



Next: Die Fluktuationen. Eigenfunktionen und
Up: Operatoren für physikalische Größen
Previous: Operatoren für physikalische Größen
Contents
Jeder physikalisch messbaren Größe wird in der Quantenmechanik ein
Operator gegenübergestellt. Aus der Wahrscheinlichkeitsinterpretation
der Wellenfunktion folgt, dass wenn eine Messgröße nur eine Funktion der
Koordinaten ist, so gilt in einem Zustand mit der WF 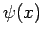
Man schreibt normalerweiser
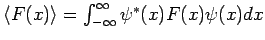 und verwendet dafür die Notation
und verwendet dafür die Notation
Bemerkung:
Oft muß man auch die Integrale
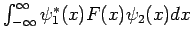 , sie sog. Matrizenelemente,
ausrechnen. Die Bezeichnung dafür ist
, sie sog. Matrizenelemente,
ausrechnen. Die Bezeichnung dafür ist
Das Skalarprodukt ist daher
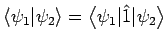 .
.
I.A. sind die Messgrößen auch die Funktionen der Impulse: wir nehmen zunächst an, dass die entsprechenden Funktionen in eine Taylor-Reihe entwickelt
werden können. Da wir noch nicht mit dem allgemeinen Formalismus
vertraut sind, sollen wir hier zunächst einen Trick anwenden.
Das Verhalten des Teilchens in einem Potential kann dirch einem Wellenpaket
oder einer stehenden Welle (Zustände des diskreten Spektrums) beschrieben
werden. Statt eines unendlichen System können wir ein sehr großes,
aber endliches System betrachten. Die Eigenschaften des physikalischen
Systems sollen nicht von der Randbedingungen sehr weit von dem Messbereich
abhängen. Daher können wir diese frei wählen. Wir betrachten nun
die periodischen Randbedingungen mit der Periode 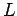 (in einem Kasten von
Volumen
(in einem Kasten von
Volumen 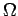 ):
):
z.B. für die freie Bewegung bekommt man die laufenden ebenen Wellen
Anhand der Randbedingungen sind nur die diskreten Werte von 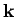 erlaubt
erlaubt
wobei
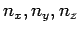 ganzen Zahlen sind: statt des kontinuierlichen
Spektrum haben wir ein diskretes Spektrum bekommen, aber für
ganzen Zahlen sind: statt des kontinuierlichen
Spektrum haben wir ein diskretes Spektrum bekommen, aber für
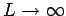 wird der Abstand zwischen den Niveaus beliebeg klein.
Wir nehmen an, dass der Grenzübergang
wird der Abstand zwischen den Niveaus beliebeg klein.
Wir nehmen an, dass der Grenzübergang
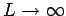 zu korrekten
Eigenschaften des kontinuierlichen Spektrum führen wird. Vorteil des
Einsperren des Systems in einen Kasten ist dass jetzt alle Wellefunktionen
normiert sind! Die normierten ebenen Wellen
zu korrekten
Eigenschaften des kontinuierlichen Spektrum führen wird. Vorteil des
Einsperren des Systems in einen Kasten ist dass jetzt alle Wellefunktionen
normiert sind! Die normierten ebenen Wellen
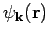 bilden einen orthonormiertes System
bilden einen orthonormiertes System
Jede in dem 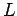 -Kasten
-Kasten 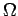 definierte Funktion kann als Summe solcher
ebenen Wellen aufgefasst werden (Fourier-Transform!):
definierte Funktion kann als Summe solcher
ebenen Wellen aufgefasst werden (Fourier-Transform!):
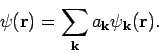 |
(24) |
Aus den Eigenschaften der diskreten Fourier-Transformation kennt man dass
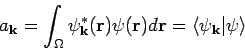 |
(25) |
(und
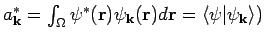 .
Durch Einsetzen der Normierungsbedingung für
.
Durch Einsetzen der Normierungsbedingung für
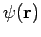 bekommen wir
bekommen wir
(die ebenen Wellen mit unterschiedlichen 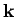 sind zueinender
orthogonal!).
sind zueinender
orthogonal!).
Für eine ebene Welle ist der Impuls
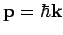 eindeutig definiert. Daher gilt für einen Wellenpaket
eindeutig definiert. Daher gilt für einen Wellenpaket
Unter Benutzung der Gl.(24) erhalten wir
Daher:
Partielle Integration in
![$\int_{\Omega }\left[ \nabla \psi _{\mathbf{k}}^{*}
(\mathbf{r})\right] \psi (\mathbf{r})d\mathbf{r}$](img1015.png) und die Annahme von
periodischen Randbedingungen (womit das Oberflächenintegral
verschwindet) ergibt
und die Annahme von
periodischen Randbedingungen (womit das Oberflächenintegral
verschwindet) ergibt
Dann:
(um zu sehen, dass
ist,
genügt es
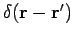 nach dem vollständigen
Funktionssystem von
nach dem vollständigen
Funktionssystem von
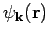 zu entwickeln:
zu entwickeln:
Gl.(24), mit
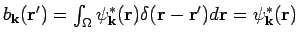 , Gl.(25)). In gleicher Weise kann man
eine beliebige Potenz des Impulses bestimmen:
, Gl.(25)). In gleicher Weise kann man
eine beliebige Potenz des Impulses bestimmen:
Z.B. ist die kinetische Energie
Wenn der Operator 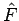 nicht selbstadjungiert ist, ist es möglich einen hermitesch konjungierten Operator
nicht selbstadjungiert ist, ist es möglich einen hermitesch konjungierten Operator 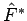 zu
definieren:
zu
definieren:
(es gilt gleichermassen
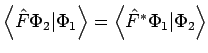 ). Die hermiteschen Operatoren sind solche, dass
). Die hermiteschen Operatoren sind solche, dass
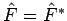 .
.
- Ein zu dem Produkt zweier Operatoren
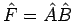 konjugierter
Operator ist
konjugierter
Operator ist
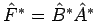 . Um das zu sehen
definieren wir
. Um das zu sehen
definieren wir
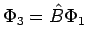 , so dass
, so dass
- Das Produkt selbstadjungierter Operatoren
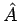 and
and 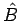 ist
selbstadjungiert, wenn diese Operatoren miteinander vertauschbar sind,
ist
selbstadjungiert, wenn diese Operatoren miteinander vertauschbar sind,
![$\left[ \hat{A},\hat{B}\right] =0$](img1041.png) , da für jedes
, da für jedes 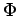 gelten muß:
gelten muß:




Next: Die Fluktuationen. Eigenfunktionen und
Up: Operatoren für physikalische Größen
Previous: Operatoren für physikalische Größen
Contents
Prof. Igor Sokolov
2005-02-14
![]()
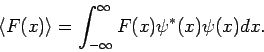
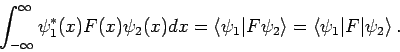
![]() (in einem Kasten von
Volumen
(in einem Kasten von
Volumen ![]() ):
):
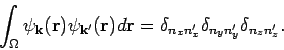
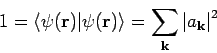
![]() eindeutig definiert. Daher gilt für einen Wellenpaket
eindeutig definiert. Daher gilt für einen Wellenpaket
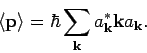
![\begin{displaymath}
\left\langle \mathbf{p}\right\rangle =-i\hbar \sum_{\mathbf{...
...thbf{k}}^{*}
(\mathbf{r})\right] \psi (\mathbf{r})d\mathbf{r.}
\end{displaymath}](img1014.png)
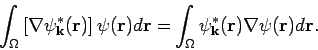
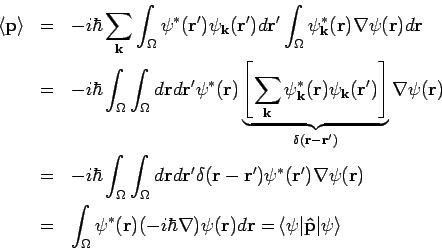
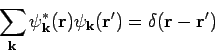
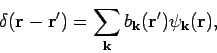
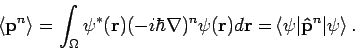
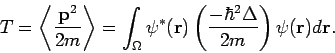
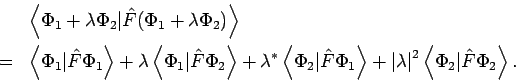
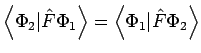 . Diese Beziehung wird oft als Definition eines
hermiteschen Operators benutzt.
. Diese Beziehung wird oft als Definition eines
hermiteschen Operators benutzt.
![]() nicht selbstadjungiert ist, ist es möglich einen hermitesch konjungierten Operator
nicht selbstadjungiert ist, ist es möglich einen hermitesch konjungierten Operator ![]() zu
definieren:
zu
definieren:
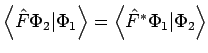 ). Die hermiteschen Operatoren sind solche, dass
). Die hermiteschen Operatoren sind solche, dass
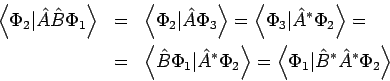
![$\left[ \hat{A},\hat{B}\right] =0$](img1041.png) , da für jedes
, da für jedes