



Next: Beispiel: das Drehmoment
Up: Operatoren für physikalische Größen
Previous: Die Mittelwerte der Funktionen
Contents
Man kann die mittlere quadratische Abweichung der Messbaren (Messgrößen) 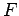 von ihrem
Mittelwert
von ihrem
Mittelwert
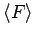 in einem durch eine Wellenfunktion
in einem durch eine Wellenfunktion
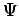 definierten Zustand bestimmen. Die Abweichung ist
definierten Zustand bestimmen. Die Abweichung ist
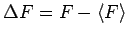 , der zugehörige hermiteschen
Operator ist
, der zugehörige hermiteschen
Operator ist
Der Operator
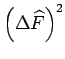 ist auch hermitesch, und
ist auch hermitesch, und
und wird durch das Integral
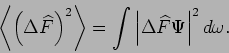 |
(26) |
Wir interessieren uns für die Situationen, wenn der Wert von 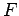 scharf
definiert wird, d.h.
scharf
definiert wird, d.h.
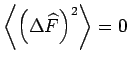 . Da der Integrand in Gl.(26) eine nicht-negativ
definierte Größe ist, kann dieser nur dann verschwinden, wenn
. Da der Integrand in Gl.(26) eine nicht-negativ
definierte Größe ist, kann dieser nur dann verschwinden, wenn
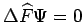 , d.h.
, d.h.
Die besonderen Werte der Parameter
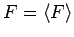 sind die
Eigenwerte des Operators
sind die
Eigenwerte des Operators 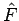 , die entsprechenden Funktionen
, die entsprechenden Funktionen 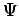 sind seine Eigenfunktionen. Z.B. die Energien der diskreten Atomzustände sind die Eigenwerte des Hamiltonians. Die Gesamtheit der Eigenwerte
stellt das Spektrum des Operators dar. Man unterscheidet zwischen dem diskreten
und dem kontinuierlichen Spektrum.
sind seine Eigenfunktionen. Z.B. die Energien der diskreten Atomzustände sind die Eigenwerte des Hamiltonians. Die Gesamtheit der Eigenwerte
stellt das Spektrum des Operators dar. Man unterscheidet zwischen dem diskreten
und dem kontinuierlichen Spektrum.




Next: Beispiel: das Drehmoment
Up: Operatoren für physikalische Größen
Previous: Die Mittelwerte der Funktionen
Contents
Prof. Igor Sokolov
2005-02-14
![]() von ihrem
Mittelwert
von ihrem
Mittelwert
![]() in einem durch eine Wellenfunktion
in einem durch eine Wellenfunktion
![]() definierten Zustand bestimmen. Die Abweichung ist
definierten Zustand bestimmen. Die Abweichung ist
![]() , der zugehörige hermiteschen
Operator ist
, der zugehörige hermiteschen
Operator ist
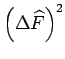 ist auch hermitesch, und
ist auch hermitesch, und
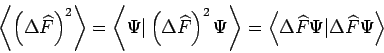
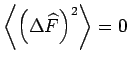 . Da der Integrand in Gl.(26) eine nicht-negativ
definierte Größe ist, kann dieser nur dann verschwinden, wenn
. Da der Integrand in Gl.(26) eine nicht-negativ
definierte Größe ist, kann dieser nur dann verschwinden, wenn