Next: Das Rietz'sche Variationsverfahren:
Up: Die Wellenmechanik
Previous: Die Wellenmechanik
Contents
Die WF in Koordinatendarstellung gehören einem Funktionalen Raum der
Funktionen, die normierbar sind (wenigstens, wenn es um die gebundenen
Zustände geht):
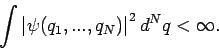 |
(34) |
(die genaue Normierung auf 1 kann dann nachträglich erfolgen). Solch eine
Annahme beschränkt unsere Betrachtung zunächst auf die Zustände
des kontinuierlichen Spektrums. In kurvelinearen Koordinaten soll man in Gl.
(33) und (34)
für 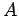 und
und 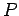 den Gewichtsfaktor für
das Volumenelement
den Gewichtsfaktor für
das Volumenelement
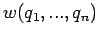 nicht vergessen. Im Folgenden
betrachten wir alles in 1D-Notation.
nicht vergessen. Im Folgenden
betrachten wir alles in 1D-Notation.
Das Gleiche gilt für alle anderen Hamilton-Operatoren, die
Hermite'sche Differentialoperatoren 2. Ordnung sind. Anhand der STURM-LIOUVILLE Theorie für die Ls'gen der ODE 2. Ordnung (d.h.
zeitunabhängigen Schrödinger-Gl.) besitzen solche Operatoren
folgenden drei Eigenschaften
- Ihre Eigenwerte sind reell
- Ihre Eigenfunktionen
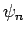 sind auf dem Definitionsinterval
sind auf dem Definitionsinterval ![$%
[a,b]$](img1264.png) orthogonal
orthogonal
- Ihre Eigenfunktionen bilden einen vollständigen Satz, d.h. jede
''nichtpathologische'' (d.h. wenigstens stückweise stetige) Funktion
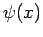 kann durch eine Reihe
kann durch eine Reihe
approximiert werden. Bemerkung: Wenn die Gesamtzahl der Eigenfkt. endlich ist, so ist
die Summe über die Gesamtzahl der linear unabhängigen Eigenfkt. zu
nehmen.
Technisch ist der Satz vollständig, wenn der Grenzwert des mittleren
quadratischen Fehlers
(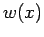 ist die Gewichtsfunktion, z.B. wenn wir die Kugelkoordinaten
benutzen). Technisch gesehen soll das Integral als Lesbegue-Integral
verstanden werden. Beweis ist technisch, siehe R. Courant und D. Hilbert,
Methods of Mathematical Physics (viele Ausgaben in Deutsch und
Englisch!) Kap. 6.
ist die Gewichtsfunktion, z.B. wenn wir die Kugelkoordinaten
benutzen). Technisch gesehen soll das Integral als Lesbegue-Integral
verstanden werden. Beweis ist technisch, siehe R. Courant und D. Hilbert,
Methods of Mathematical Physics (viele Ausgaben in Deutsch und
Englisch!) Kap. 6.
Die Koeffizienten 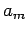 sind durch
sind durch
gegeben (folgt aus der Orthogonalität und Normierung).
Aus der Normierung von 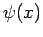 folgt
folgt
die Parceval-Identität.
Die Tatsache, dass die Eigenfunktionen ein vollständiges orthonormales
System (VONS) der Fkt. bilden hat vielerlei Bedeutung, z.B. für das




Next: Das Rietz'sche Variationsverfahren:
Up: Die Wellenmechanik
Previous: Die Wellenmechanik
Contents
Prof. Igor Sokolov
2005-02-14
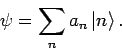
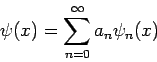
![\begin{displaymath}
\lim_{m\rightarrow 0}\int_{a}^{b}\left[ \psi (x)-\sum_{n=0}^{m}a_{n}\psi
_{n}(x)\right] ^{2}w(x)dx=0
\end{displaymath}](img1266.png)
![]() sind durch
sind durch
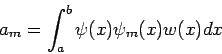
![]() folgt
folgt