



Next: Effekte außerhalb der Reichweite
Up: Lichtwellen
Previous: Interferenz und Beugung
Contents
Die typische Situation entspricht einem Wellenpaket einer
endllichen räumlichen / zeitlichen Ausdehnung.
Wir betrachten jetzt eine eindimensionale Situation. Nehmen wir an, die
Fkt. 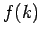 ist groß im
ist groß im 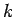 -Bereich von der Breite
-Bereich von der Breite 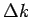 um
irgendeinen Wert
um
irgendeinen Wert 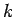 . Die Abschätzung des Integrals mit der Methode der
stat. Phase ergibt, dass der maximale Beitrag von der Welle mit der
konstanten Phase
. Die Abschätzung des Integrals mit der Methode der
stat. Phase ergibt, dass der maximale Beitrag von der Welle mit der
konstanten Phase
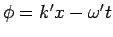 kommt, wenn es
nicht mehr als 1 Oszillation in dem Bereich
kommt, wenn es
nicht mehr als 1 Oszillation in dem Bereich 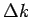 gibt (wenn es in
diesem Bereich viele Oszillationen der Exponentiafkt. gibt, kompensieren Sie
einender, und der Beitrag solcher Schwingungen ist klein). D.h.
gibt (wenn es in
diesem Bereich viele Oszillationen der Exponentiafkt. gibt, kompensieren Sie
einender, und der Beitrag solcher Schwingungen ist klein). D.h.
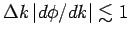 .
.
Da
ist die Welle lokalisiert im räumlichen Bereich mit der Abmessung
um die Mitte des Wellenpakets, das sich anhand der Gl.
bewegt. Das definitert die Gruppengeschwindigket
Beispiel: Ein Gausspaket.
![$f(k^{\prime })=\frac{A}{\sqrt{2\pi }\Delta
k}\exp \left[ -(k^{\prime }-k)^{2}/2(\Delta k)^{2}\right] $](img65.png) . In diesem Fall
ist das entsprechende Integral analytisch zu bestimmen:
. In diesem Fall
ist das entsprechende Integral analytisch zu bestimmen:
a) ohne Dispersion (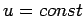 )
)
Das Quadrat der Amplitude (''Intensität'')
beschreibt eine Umschlagsfunktion des Wellenpakets von räumlichen
Ausdehnung
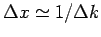 , deren Mitte sich mit der
geschwindigkeit
, deren Mitte sich mit der
geschwindigkeit 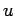 bewegt.
bewegt.
b) mit Dispersion:
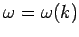 .
.
mit
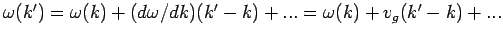 . Variablenwechsel:
. Variablenwechsel:
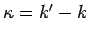 .
Dann erhalten wir
.
Dann erhalten wir
und
Die entsprechnde Amplitude (Umschlagsfunktion) beschreibt einen Wellenzug von
räumlicher Ausdehnung
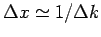 , deren Mitte sich mit
der Geschwindigkeit
, deren Mitte sich mit
der Geschwindigkeit 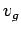 bewegt (Gruppengeschwindigkeit). Die endliche
Kohärenzlänge bewirkt z.B. die Abschwächung der Nebenmaxima bei
einer Beugung am Diffraktionsgitter.
bewegt (Gruppengeschwindigkeit). Die endliche
Kohärenzlänge bewirkt z.B. die Abschwächung der Nebenmaxima bei
einer Beugung am Diffraktionsgitter.
2. Woche




Next: Effekte außerhalb der Reichweite
Up: Lichtwellen
Previous: Interferenz und Beugung
Contents
Prof. Igor Sokolov
2005-02-14
![]() ist groß im
ist groß im ![]() -Bereich von der Breite
-Bereich von der Breite ![]() um
irgendeinen Wert
um
irgendeinen Wert ![]() . Die Abschätzung des Integrals mit der Methode der
stat. Phase ergibt, dass der maximale Beitrag von der Welle mit der
konstanten Phase
. Die Abschätzung des Integrals mit der Methode der
stat. Phase ergibt, dass der maximale Beitrag von der Welle mit der
konstanten Phase
![]() kommt, wenn es
nicht mehr als 1 Oszillation in dem Bereich
kommt, wenn es
nicht mehr als 1 Oszillation in dem Bereich ![]() gibt (wenn es in
diesem Bereich viele Oszillationen der Exponentiafkt. gibt, kompensieren Sie
einender, und der Beitrag solcher Schwingungen ist klein). D.h.
gibt (wenn es in
diesem Bereich viele Oszillationen der Exponentiafkt. gibt, kompensieren Sie
einender, und der Beitrag solcher Schwingungen ist klein). D.h.
![]() .
.
![]() )
)
![\begin{eqnarray*}
\Psi (x,t) &=&\int f(k^{\prime })e^{ik^{\prime }(x-ut)}dk^{\pr...
...
&=&Ae^{ik(x-ut)}\exp \left[ -(\Delta k)^{2}(x-ut)^{2}\right] .
\end{eqnarray*}](img67.png)
![]() .
.
![\begin{eqnarray*}
\Psi (x,t) &=&\int f(k^{\prime })e^{i(k^{\prime }x-\omega (k^{...
...2}}\right] e^{ik^{\prime }(x-\omega (k^{\prime
})t)}dk^{\prime }
\end{eqnarray*}](img72.png)
![\begin{eqnarray*}
\Psi (x,t) &=&\frac{A}{\sqrt{2\pi }\Delta k}\int \exp \left[
...
... Ae^{ik(x-ut)}\exp \left[ -(\Delta k)^{2}(x-v_{g}t)^{2}\right] .
\end{eqnarray*}](img75.png)