



Next: Angeregte Zustände
Up: Das Rietz'sche Variationsverfahren:
Previous: Das Rietz'sche Variationsverfahren:
Contents
Zur Berechnung der Energie 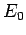 des Grundzustandes benutzt man die
Ungleichung:
des Grundzustandes benutzt man die
Ungleichung:
für beliebige, die Randbedingungen erfüllende 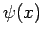 . Beweis ist
einfach: Da
. Beweis ist
einfach: Da
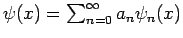 , gilt anhand
der Orthonormalitätseigenschaft
, gilt anhand
der Orthonormalitätseigenschaft
Daher gilt
(z.B.
mit
Zur praktischen Berechnung der Energie des Grundzustandes wählt man eine
Testfunktion
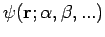 , mit
, mit
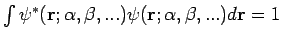 , die von Parametern
, die von Parametern
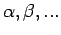 abhängig ist und
die Randbedingungen erfüllt, und berechnet das Integral
abhängig ist und
die Randbedingungen erfüllt, und berechnet das Integral
Dann berechnet man die Parameter
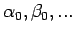 , die
, die
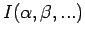 minimieren,
minimieren,
und
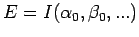 als die Näherung für die
Energie des Grundzustandes benutzt. Hat man Glück, bekommt man eine
hervorragende Näherung schon mit einem Parameter.
als die Näherung für die
Energie des Grundzustandes benutzt. Hat man Glück, bekommt man eine
hervorragende Näherung schon mit einem Parameter.
Beispiel: Grundzustand des harmonischen Oszillators: in
dimensionslosen Koordinaten
Die natürlichen Randbedingungen entsprechen
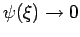 für
für
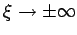 . Die WF des Grundzustands ist,
bekannterweise, eine Gaußglocke
. Die WF des Grundzustands ist,
bekannterweise, eine Gaußglocke
Die entsprechende Energie 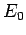 ist genau 1/2 (in Einheiten von
ist genau 1/2 (in Einheiten von 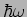 ).
).
Wählen wir unsere Testfunktion in Form
die die Randbedingungen erfüllt und die Tatsache berücksichtigt,
dass die entsprechende WF gerade sein muss. Dann
Das Minimieren ergibt den genauen Wert von 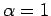 und
und 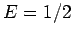 . In
diesem Fall stimmt die Testfunktion (und die Energie) mit exakten Werten
überein.
. In
diesem Fall stimmt die Testfunktion (und die Energie) mit exakten Werten
überein.
Nehmen wir z.B. eine Testfunktion
(auch eine symmetrische Glocke, auf 1 normiert:
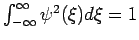 , sonst ähnelt sie nicht besonders der
richtigen WF). Die Energie ist dann
, sonst ähnelt sie nicht besonders der
richtigen WF). Die Energie ist dann
Die ist minimiert für 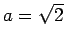 , und entspricht
, und entspricht 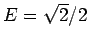 , 41%
höher als die genaue Energie. Die Wahl der Testfunktion war nicht
besonders günstig, da sie für
, 41%
höher als die genaue Energie. Die Wahl der Testfunktion war nicht
besonders günstig, da sie für
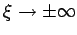 zu
langsam abfällt.
zu
langsam abfällt.




Next: Angeregte Zustände
Up: Das Rietz'sche Variationsverfahren:
Previous: Das Rietz'sche Variationsverfahren:
Contents
Prof. Igor Sokolov
2005-02-14
![]() des Grundzustandes benutzt man die
Ungleichung:
des Grundzustandes benutzt man die
Ungleichung:
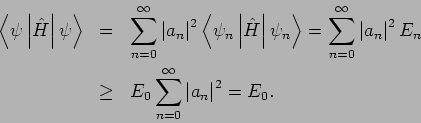
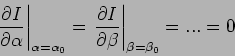
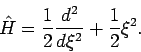
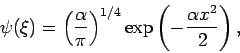
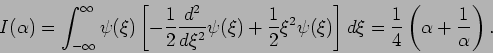
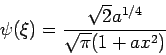
![\begin{displaymath}
I(a)=\int_{-\infty }^{\infty }\psi (\xi )\left[ -\frac{1}{2}...
...c{1}{2}\xi ^{2}\psi (\xi )\right] d\xi =\frac{%
2+a^{2}}{4a}.
\end{displaymath}](img1294.png)