



Next: Allgemeine Struktur der Quantenmechanik
Up: Das Rietz'sche Variationsverfahren:
Previous: Energie des Grundzustandes
Contents
Bezeichnen wir die Wellenfunktion des Grundzustands durch 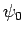 . Es
gilt dann
. Es
gilt dann
mit
(Beweis genau wie bei dem Grundzustand, unter Berücksichtigung der
Orthogonalität). Gleichermassen kann man die Variationsprinzipien
für die höheren Zustände formulieren, indem man die WFen annimmt,
die zu den WFen aller darunterliegenden Zustände orthogonal sind. Das ist
bedeutend komplizierter als das Variationsverfahren für den
Grundzustand. In einigen Fällen sind die Orthogonalitätsbedingungen
bei geeigneter Wahl der Testfunktionen anhand der Symmetrieeigenschaften
erfüllt.
Beispiel: 1. angeregte Zustand für den harmonische Oscillator.
Anhand der Symmetrie des Potentials ist die WF des Grundzustandes eine
gerade Funktion von 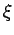 . Die Funktion des 1 angeregten Zustandes ist dann
ungerade, und deswegen der WF des Grundzustandes automatisch orthogonal.
Anhand des Knotensatzes hat diese Funktion einen Knoten. Einfachste Form:
. Die Funktion des 1 angeregten Zustandes ist dann
ungerade, und deswegen der WF des Grundzustandes automatisch orthogonal.
Anhand des Knotensatzes hat diese Funktion einen Knoten. Einfachste Form:
Man bekommt
Das Minimieren ergibt 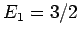 (in Einheiten von
(in Einheiten von 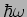 ).
).
Prof. Igor Sokolov
2005-02-14
![]() . Es
gilt dann
. Es
gilt dann
![]() . Die Funktion des 1 angeregten Zustandes ist dann
ungerade, und deswegen der WF des Grundzustandes automatisch orthogonal.
Anhand des Knotensatzes hat diese Funktion einen Knoten. Einfachste Form:
. Die Funktion des 1 angeregten Zustandes ist dann
ungerade, und deswegen der WF des Grundzustandes automatisch orthogonal.
Anhand des Knotensatzes hat diese Funktion einen Knoten. Einfachste Form:
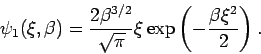
![\begin{displaymath}
I_{1}(\beta )=\int_{-\infty }^{\infty }\psi _{1}(\xi ,\beta ...
...t] d\xi =\frac{3}{4}\left( \beta +\frac{1}{\beta }%
\right) .
\end{displaymath}](img1301.png)