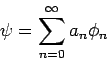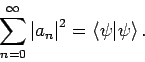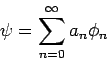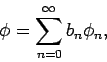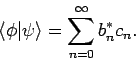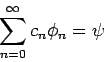Next: Hermite'sche Operatoren. Fall des
Up: Allgemeine Struktur der Quantenmechanik
Previous: Allgemeine Struktur der Quantenmechanik
Contents
Axiomen:
1. 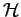 ist ein komplexer, linearer Vektorraum.
ist ein komplexer, linearer Vektorraum.
- Er ist bezüglich zwei Verknüpfungen, der Addition und
Multiplikation mit einer Zahl, abgeschlossen:
- Diese Operationen besitzen die üblichen Eigenschaften der
- Assoziativität und Kommutativität bzgl. Addition
- Existenz des Nullelements
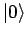 (bzgl. der Addition)
(bzgl. der Addition)
- Existenz des inversen Elements bzgl. Addition
- Distributivität bzgl. Multiplikation.
Die Elemente
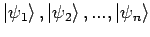 heißen linear
unabhängig falls die Reaktion
heißen linear
unabhängig falls die Reaktion
nur durch
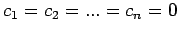 erfüllbar ist. Als Dimension von
erfüllbar ist. Als Dimension von 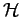 bezeichnet man die Maximalzahl linear-unabhängiger
Elemente in
bezeichnet man die Maximalzahl linear-unabhängiger
Elemente in 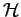 . Wenn es unendlich viele
linear-unabhängige Elementen gibt ist der Raum unendlich-dimensional.
. Wenn es unendlich viele
linear-unabhängige Elementen gibt ist der Raum unendlich-dimensional.
Bemerkung: Vorläufig setzen wir die Wellenfunktion 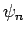 und den Zustandsvektor
und den Zustandsvektor
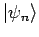 gleich.
gleich.
2. 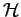 ist ein unitärer Raum, d.h.
ist ein unitärer Raum, d.h.
- Es wird ein Skalarprodukt zw. zwei Vektoren
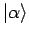 und
und
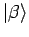 definiert als eine komplexen Zahl
definiert als eine komplexen Zahl
In Koordinatendarstellung
-
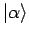 und
und
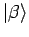 heißen orthogonal falls
heißen orthogonal falls
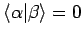 .
.
- Norm von Vektor
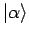 :
:
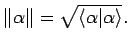
- Schwarz'sche Ungleichung
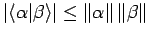
- Dreiecksungleichung
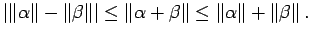
Diese Eigenschaften definieren einen komplexen linearen Vektorraum. Der
Hilbert-Raum besitzt zusätzliche Eigenschaften.
Folgen in 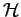 .
.
Die Folge
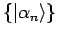 konvergiert
stark gegen
konvergiert
stark gegen
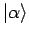 falls
falls
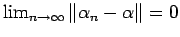 .
.
Eine Folge
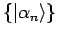 heißt
Cauchy-Folge, falls es zu jedem
heißt
Cauchy-Folge, falls es zu jedem
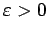 eine ganze Zahl
eine ganze Zahl
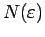 gibt, so dass
gibt, so dass
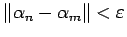 für
für
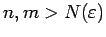 . Jede stark konvergierende
Folge ist auch eine Cauchy-Folge.
. Jede stark konvergierende
Folge ist auch eine Cauchy-Folge.
3. 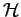 ist separabel: Jede
ist separabel: Jede
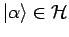 ist ein Limes einer Cauchy-Folge in
ist ein Limes einer Cauchy-Folge in 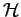 .
.
4. 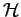 ist vollständig: Jede Cauchy-Folge
ist vollständig: Jede Cauchy-Folge
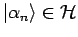 konvergiert gegen
konvergiert gegen
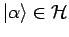 .
.
Aus 3 und 4 folgt die Existenz des vollständigen Orthonormalsystems
(VONS) der Basisvektoren
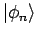 aus
aus 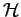 :
eine Menge M der Vektoren, für die es kein Element aus
:
eine Menge M der Vektoren, für die es kein Element aus 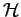 gibt,
das nicht zu M gehört, jedoch orthogonal zu allen Elementen aus M ist.
Die Vektoren von M sind linear unabhängig.
gibt,
das nicht zu M gehört, jedoch orthogonal zu allen Elementen aus M ist.
Die Vektoren von M sind linear unabhängig.
Unendlich- (abzählbar-) dimensionaler Hilbert Raum 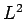 (
(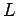 steht
für Lesbegue,
steht
für Lesbegue, 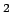 - für die quadratische Norm) ist der gültige
WF-Raum der Quantenmechanik, sieh J. von Neumann: Mathematische
Grundlagen der Quantenmechanik, Springer, Berlin, 1968.
- für die quadratische Norm) ist der gültige
WF-Raum der Quantenmechanik, sieh J. von Neumann: Mathematische
Grundlagen der Quantenmechanik, Springer, Berlin, 1968.
- Das wichtigste, was daraus folgt, ist die Tatsache, dass für
jede beliebige Funktion aus
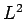 eine Entwicklung nach einem VONS der
Basisfunktionen
eine Entwicklung nach einem VONS der
Basisfunktionen 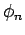 existiert:
existiert:
mit
Die Wahl von verschiedenen Basisvektoren entspricht den verschiedenen
Darstellungen. Die Tatsache, dass die Funktionen aus 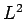 stets eine
endliche Norm besitzen, begrenzt zunächst unsere Ausführungen auf
die Zuständen des diskteten Spektrums.
stets eine
endliche Norm besitzen, begrenzt zunächst unsere Ausführungen auf
die Zuständen des diskteten Spektrums.
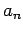 genügen den Parceval-Identität
genügen den Parceval-Identität
- Wenn
und
so
- Wenn eine Reihe
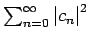 gegen
einem Zahl
gegen
einem Zahl 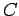 konvergiert, so konvergiert die Funktionsreihe
konvergiert, so konvergiert die Funktionsreihe
gegen eine Funktion
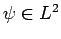 mit einer Norm
mit einer Norm 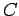 .
.




Next: Hermite'sche Operatoren. Fall des
Up: Allgemeine Struktur der Quantenmechanik
Previous: Allgemeine Struktur der Quantenmechanik
Contents
Prof. Igor Sokolov
2005-02-14
![]() ist ein komplexer, linearer Vektorraum.
ist ein komplexer, linearer Vektorraum.
![]() heißen linear
unabhängig falls die Reaktion
heißen linear
unabhängig falls die Reaktion
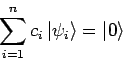
![]() und den Zustandsvektor
und den Zustandsvektor
![]() gleich.
gleich.
![]() ist ein unitärer Raum, d.h.
ist ein unitärer Raum, d.h.
![]() .
.
![]() konvergiert
stark gegen
konvergiert
stark gegen
![]() falls
falls
![]() .
.
![]() heißt
Cauchy-Folge, falls es zu jedem
heißt
Cauchy-Folge, falls es zu jedem
![]() eine ganze Zahl
eine ganze Zahl
![]() gibt, so dass
gibt, so dass
![]() für
für
![]() . Jede stark konvergierende
Folge ist auch eine Cauchy-Folge.
. Jede stark konvergierende
Folge ist auch eine Cauchy-Folge.
![]() ist separabel: Jede
ist separabel: Jede
![]() ist ein Limes einer Cauchy-Folge in
ist ein Limes einer Cauchy-Folge in ![]() .
.
![]() ist vollständig: Jede Cauchy-Folge
ist vollständig: Jede Cauchy-Folge
![]() konvergiert gegen
konvergiert gegen
![]() .
.
![]() aus
aus ![]() :
eine Menge M der Vektoren, für die es kein Element aus
:
eine Menge M der Vektoren, für die es kein Element aus ![]() gibt,
das nicht zu M gehört, jedoch orthogonal zu allen Elementen aus M ist.
Die Vektoren von M sind linear unabhängig.
gibt,
das nicht zu M gehört, jedoch orthogonal zu allen Elementen aus M ist.
Die Vektoren von M sind linear unabhängig.
![]() (
(![]() steht
für Lesbegue,
steht
für Lesbegue, ![]() - für die quadratische Norm) ist der gültige
WF-Raum der Quantenmechanik, sieh J. von Neumann: Mathematische
Grundlagen der Quantenmechanik, Springer, Berlin, 1968.
- für die quadratische Norm) ist der gültige
WF-Raum der Quantenmechanik, sieh J. von Neumann: Mathematische
Grundlagen der Quantenmechanik, Springer, Berlin, 1968.