



Next: Statistische Verteilung der Messresultate
Up: Formalismus der Quantenmechanik und
Previous: Der Begriff des Hilbert-Raums
Contents
Wir betrachten einen Hermite'schen Operator  , der auf die Funktionen
aus dem Hilbert-Raum wirkt:
, der auf die Funktionen
aus dem Hilbert-Raum wirkt:
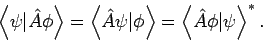
Betrachten wir die Eigenfkt.
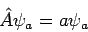
mit
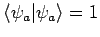 . Daher gilt:
. Daher gilt:
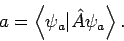
Dieser Wert ist reell nach der Definition des Hermite'schen Operators.
- Die Eigenfunktionen, die zu der unterschiedlichen Eigenwerten
gehöhren, sind orthogonal:
Bilden wir die Skalarprodukte
und
so dass
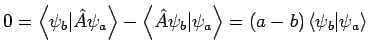 . Daraus folgt, dass für
. Daraus folgt, dass für 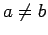 gilt
gilt
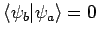 .
. 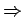 Eigenfunktionen, die zu verschiedenenen Eigenwerten gehören, sind
linear unabhängig.
Eigenfunktionen, die zu verschiedenenen Eigenwerten gehören, sind
linear unabhängig.
- Die Eigenwerte bilden eine diskrete Folge (endlich oder
abzählbar).
- Wenn der Eigenwert
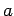
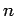 -fach entartet ist, kann jede Eigenfunktion
als eine lineare Kombination aus
-fach entartet ist, kann jede Eigenfunktion
als eine lineare Kombination aus 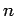 linear-unabhängigen Funktionen
linear-unabhängigen Funktionen
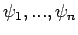 dargestellt werden. Aus diesen Funktionen kann man immer durch
Schmidt-Orthogonalisierung ein orthonormales System
dargestellt werden. Aus diesen Funktionen kann man immer durch
Schmidt-Orthogonalisierung ein orthonormales System
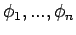 bilden: Man nehme
bilden: Man nehme
mit
Die Fkt. 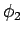 wird gegeben durch
wird gegeben durch
Da 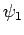 (und somit
(und somit 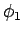 ) und
) und 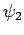 linear unabhängig
sind, ist
linear unabhängig
sind, ist
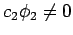 . Normierung:
. Normierung: 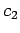 ist, bis auf eine Phase,
durch
ist, bis auf eine Phase,
durch
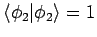 gegeben. Weiterhin,
gegeben. Weiterhin,
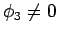 (anhand der linearen Unabhängigkeit) und kann normiert
werden, u.s.w. bis
(anhand der linearen Unabhängigkeit) und kann normiert
werden, u.s.w. bis 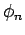 . Es gilt:
. Es gilt:
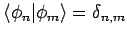 .
.
- Auch wenn Entartungsgrad unendlich ist, ist es möglich eine
unendliche Folge der orthonormierten Funktionen
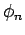 zu bilden. Jede
Funktion, die zum Eigenwert
zu bilden. Jede
Funktion, die zum Eigenwert 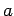 gehört, kann durch eine Reihe über
diese Funktionen dargestellt werden.
gehört, kann durch eine Reihe über
diese Funktionen dargestellt werden.
Subsections




Next: Statistische Verteilung der Messresultate
Up: Formalismus der Quantenmechanik und
Previous: Der Begriff des Hilbert-Raums
Contents
Prof. Igor Sokolov
2005-02-14
![]() , der auf die Funktionen
aus dem Hilbert-Raum wirkt:
, der auf die Funktionen
aus dem Hilbert-Raum wirkt:
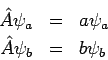
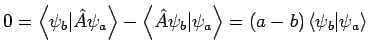 . Daraus folgt, dass für
. Daraus folgt, dass für