Betrachten wir das Eigenwertproblem
dem diskreten Spektrum ![]() mit entweder endlichen oder abzählbaren
Menge von Werten
mit entweder endlichen oder abzählbaren
Menge von Werten
Kontinuierlichem Spektrum ![]() , das durch einen kontinuierlichen Index
, das durch einen kontinuierlichen Index
![]() numeriert ist.
numeriert ist.
Den disktereten Fall haben wir schon diskutiert.
Im kontinuierlichen Fall ist ![]() eine Eigenfkt. zum Eigenwert
eine Eigenfkt. zum Eigenwert
![]() . Die Norm von dieser Fkt. ist unendlich. Wir nehmen aber an dass das
Eigendifferential
. Die Norm von dieser Fkt. ist unendlich. Wir nehmen aber an dass das
Eigendifferential
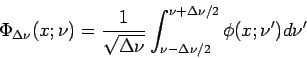
So sind z.B. die Eigenfunktionen der Impulsoperators. Alle für den
Hilbert-Raum kennzeichnenden Eigenschaften gelten dann nicht für die
WF'nen selbst, sondern für die Eigendifferentiale. Das skalare Produkt
von der Funktion selbst ist auf eine ![]() -Funktion normiert:
-Funktion normiert:
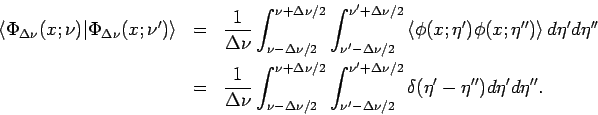
Bemerkung: Wenn ![]() Impuls wäre, so entspräche das
Eigendifferential einem Wellenpaket mit endlicher Breite
Impuls wäre, so entspräche das
Eigendifferential einem Wellenpaket mit endlicher Breite ![]() im
Impulsraum, und ist deswegen von einer endlichen Ausdehnung
im
Impulsraum, und ist deswegen von einer endlichen Ausdehnung
![]() in Ortsraum. Solches Paket ist normierbar (1 Teilchen).
in Ortsraum. Solches Paket ist normierbar (1 Teilchen).
![]() (und entspr.
(und entspr. ![]() ) muss viel größer sein als alle
andere typische Abmessumgen der Problems. Daher entspricht die Betrachtung
der Eigendifferentiale der Formalisierung von unserer früheren
Wellenpaketvorstellung.
) muss viel größer sein als alle
andere typische Abmessumgen der Problems. Daher entspricht die Betrachtung
der Eigendifferentiale der Formalisierung von unserer früheren
Wellenpaketvorstellung.
Die EFs des diskreten und kontinuierlichen Spektrums zusammen bilden einen
erweiterten Hilbert-Raum, so dass insgesamt, für jede ![]()
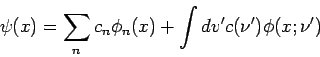
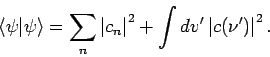
Bemerkung: Nicht alle Hermiteschen Operatoren besitzen ein VON-System der Eigenfunktionen. Alle Operatoren, die die physikalische Messbaren darstellen, besitzen solche.