Statistik der Messwerten im allgemeinen Fall.

Alle vorherigen Resultate basieren auf der Annahme, dass das Funktionensystem $\phi _{n}$ ein vollständiges System ist. Wir können diese Resultaten nicht sofort auf den Fall des kontinuierlichen Spektrums ausweiten: Die WF des kontinuierlichen Spektrums sind nicht normierbar. Solche Normierung kann aber durch einen mathematischen Trick ''erzwungen'' werden. Die weitere Betrachtung ist mathematisch nicht rigoros, die exaktere folgt durch genauere Definition der verallgemeinerten Funktionen (Distributionen).

Beispiel: der Impulsoperator. Betrachten wir die Eigenfunktion $% \phi _{p}(x)$ des Impulsoperators $\hat{p}=-i\hbar \frac{\partial }{\partial x}$ mit dem Eigenwert $p$:

$$-i\hbar \frac{\partial }{\partial x}\phi (x,p)=p\phi (x,p).$$

(die Eigenfunktion ist eigentlich, bis zur Normierung, $e^{-\frac{i}{\hbar }% px}$, $p$ nimmt alle reellen Werte an). Jede beliebige WF $\psi (x)$ kann dann als

$$\psi (x)=\int_{-\infty }^{\infty }c(p)\phi (x,p)dp$$ (35)

präsentiert werden. $\left\vert c(p)\right\vert ^{2}dp$ soll man als Wahrscheinlichkeit sehen, einen Wert von $p$ im Intervall $(p,p+dp)$ zu finden. Der Koeffizient $c(p)$ soll als Skalarprodukt

$$c(p)=\left\langle \phi (x,p)\vert\psi (x)\right\rangle$$

interprätiert werden. Wenn wir jetzt die Gl.(35) in diesen Ausdruck einsetzen, bekommen wir

$$c(p)=\int_{-\infty }^{\infty }c(p^{\prime })\left\langle \ph... ...\phi (x,p^{\prime \prime })\right\rangle dp^{\prime \prime }.$$

Diese Eigenschaft soll für jede quadrat integrable Fkt. im Impulsraum gelten. Es existiert keine ''reguläre'' Fkt. $f(p^{\prime },p^{\prime \prime })$, die solche Eigenschaft besitzt. Man kann aber eine verallgemeinerte Fkt. $\delta (x)$ einführen, so dass

$$\int_{a}^{b}g(x)\delta (x-x_{0})dx=\left\{ \begin{array}{l}... ...,\quad x_{0}\in (a,b) \\ 0,\quad sonst. \end{array}\right. .$$

Unter Benutzung der $\delta$-Fkt. erfolgt die Normierung

$$\phi (x,p)=\frac{1}{\sqrt{2\pi \hbar }}e^{ipx/\hbar }.$$

Uneigentliche Zustandsvektoren sind auf $\delta$-Funktion normiert

$$\left\langle \phi (x,p)\vert\phi (x,p^{\prime })\right\rangl... ... }\phi ^{*}(x,p)\phi (x,p^{\prime })dx=\delta (p-p^{\prime })$$

(i.e. das Skalarprodukt ist 0 falls $p\neq p^{\prime }$ und divergiert sonst.) Die Eigenschaften der entsprechenden Entwicklungen über die EF vom Impulsoperator sind durch die Theorie der Fourier-Integrale bekannt.

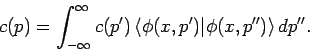
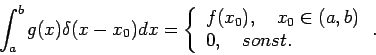
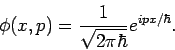
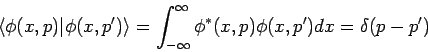
Bemerkung: Wie bei der Betrachtung des Impulsoperators früher (Woche...), können wir das System als endlich, mit zyklischen Randbedingungen betrachten; solche Systeme haben stets nur ein diskretes Spektrum, das in einigen Teilen für wachsende Systemgröße $L$ immer dichter wird. Dabei müßen wir nicht aus der Rahmen des Hilbert-Raums der WF hinausgehen. Für Impulsoperator entspricht das der Näherung der Fourier-Integral für eine nicht-periodiche Funktion durch eine Fourier-Reihe auf immer größeren Intervallen. In Anwendungen ist dieser Vorgang oft sogar von Vorteil. I.A. kann man den Vorgang aber auch anders formalisieren.