



Next: Unitäre Transformationen für die
Up: Darstellungen der Quantenmechanik
Previous: Bemerkungen:
Contents
Die Matrix 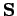 aus der Sek.(9.7) stellt i.A. keinen Operator dar:
Jeder Operator ist definiert in einer Darstellung, und
aus der Sek.(9.7) stellt i.A. keinen Operator dar:
Jeder Operator ist definiert in einer Darstellung, und 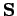 hängt von 2 Darstellungen ab. Es gibt aber die Situationen wenn
hängt von 2 Darstellungen ab. Es gibt aber die Situationen wenn 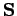 ein Operator ist. Es ist der Fall wenn zwischen den Basisvektoren in
beiden Darstellungen eine eins-zu-eins Korrespondänz besteht (dann muss
auch die Natur der Spektren gleich sein, i.e. beide diskret, mit gleichen
Anzahl der Zuständen, oder beiden kontinuierlich u.s.w.). Die
korrespondenz zwischen
ein Operator ist. Es ist der Fall wenn zwischen den Basisvektoren in
beiden Darstellungen eine eins-zu-eins Korrespondänz besteht (dann muss
auch die Natur der Spektren gleich sein, i.e. beide diskret, mit gleichen
Anzahl der Zuständen, oder beiden kontinuierlich u.s.w.). Die
korrespondenz zwischen
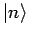 und
und
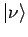 ist durch einen Operator
ist durch einen Operator 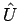 gegeben:
gegeben:
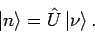
Dann ist
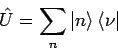
und
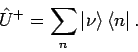
Da beide Vektorensysteme
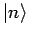 und
und
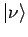 orthonormiert sind, so gilt:
orthonormiert sind, so gilt:
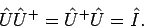
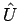 ist ein unitärer Operator. Die Matrix
ist ein unitärer Operator. Die Matrix 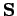 mit
Elementen
mit
Elementen
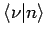 , ist die Matrix
, ist die Matrix 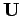 in
in 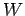 -Darstellung.Die Änderung der Darstellung entspricht in
gewissem Sinne der ''Rotation'' des Koordinatensystems der Basisvektoren.
Statt das Basissystem anhand
-Darstellung.Die Änderung der Darstellung entspricht in
gewissem Sinne der ''Rotation'' des Koordinatensystems der Basisvektoren.
Statt das Basissystem anhand
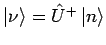 zu transformieren, kann man die Basis gleich lassen und die
Vektoren und Operatoren transformieren (''rotieren''):
zu transformieren, kann man die Basis gleich lassen und die
Vektoren und Operatoren transformieren (''rotieren''):
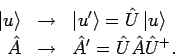
Die Skalarpodukte und die Adjunktionsbeziehungen zwischen Vektoren und
Operatoren bleiben bei solchen Transformationen erhalten, da
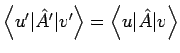 . Wenn
. Wenn 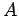 eine Messbare ist, so ist
eine Messbare ist, so ist 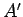 auch
eine Messbare mit dem gleichen Eigenwertspektrum. Die Eigenvektoren
auch
eine Messbare mit dem gleichen Eigenwertspektrum. Die Eigenvektoren
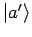 von
von
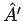 sind die transformierten
Eigenvektoren
sind die transformierten
Eigenvektoren
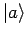 von
von  . Die Matrix
. Die Matrix
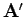 in
in 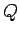 -Darstellung hat die gleiche Gestalt wie die Matrix
-Darstellung hat die gleiche Gestalt wie die Matrix 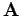 in
in 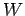 -Darstellung. Der Vektor
-Darstellung. Der Vektor
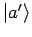 hat in
hat in 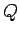 -Darstellung die gleichen Komponenten, wie der Vektor
-Darstellung die gleichen Komponenten, wie der Vektor
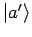 in
in 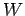 -Darstellung.
-Darstellung.
- Zwei aufeinenderfolgende unitäre Transformationen
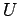 und
und 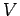 definieren eine unitäre Transformation
definieren eine unitäre Transformation 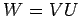 .
.
- Eine infinitesimale Transformation ist durch einen Operator
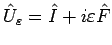 bestimmt, mit infinitesimal kleinen,
reellen
bestimmt, mit infinitesimal kleinen,
reellen 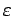 , so dass die Terme, die in
, so dass die Terme, die in 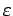 quadratisch sind, vernachlässigt werden können. Die
Forderung, dass dieser Operator unitär ist ergibt:
quadratisch sind, vernachlässigt werden können. Die
Forderung, dass dieser Operator unitär ist ergibt:
ergibt in 1. Ordnung in 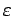
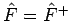 , i.e. jeder
Hermitesche Operator
, i.e. jeder
Hermitesche Operator 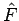 definiert eine infinitesimale
unitäre Transformation
definiert eine infinitesimale
unitäre Transformation
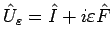 . Es gilt:
. Es gilt:
und
so dass
- Man kann diese Entwicklung bis zu höheren Glieder fortsetzen und
statt infinitesimalen
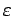 irgendeine Zahl
irgendeine Zahl 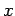 nehmen:
nehmen:
Die Einwirkung eines solches Operators auf
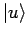 ergibt
ergibt
Die Transformation eines Operators wird dann durch
gegeben.
Die gleichzeitige Änderung der Zustandsvektoren und der Operatoren
führt zur verschiedenen Schreibweisen für einen Zustand zum
gegebenen Zeitpunkt. Diese gleichzeitige unitäre Transformation der
Wellenfunktion und der Operatoren ändert die Gestalt der
Wellenfunktionen, verändert aber den Zustand des Systems nicht.




Next: Unitäre Transformationen für die
Up: Darstellungen der Quantenmechanik
Previous: Bemerkungen:
Contents
Prof. Igor Sokolov
2005-02-14
![]() aus der Sek.(9.7) stellt i.A. keinen Operator dar:
Jeder Operator ist definiert in einer Darstellung, und
aus der Sek.(9.7) stellt i.A. keinen Operator dar:
Jeder Operator ist definiert in einer Darstellung, und ![]() hängt von 2 Darstellungen ab. Es gibt aber die Situationen wenn
hängt von 2 Darstellungen ab. Es gibt aber die Situationen wenn ![]() ein Operator ist. Es ist der Fall wenn zwischen den Basisvektoren in
beiden Darstellungen eine eins-zu-eins Korrespondänz besteht (dann muss
auch die Natur der Spektren gleich sein, i.e. beide diskret, mit gleichen
Anzahl der Zuständen, oder beiden kontinuierlich u.s.w.). Die
korrespondenz zwischen
ein Operator ist. Es ist der Fall wenn zwischen den Basisvektoren in
beiden Darstellungen eine eins-zu-eins Korrespondänz besteht (dann muss
auch die Natur der Spektren gleich sein, i.e. beide diskret, mit gleichen
Anzahl der Zuständen, oder beiden kontinuierlich u.s.w.). Die
korrespondenz zwischen
![]() und
und
![]() ist durch einen Operator
ist durch einen Operator ![]() gegeben:
gegeben:
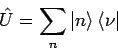
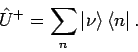
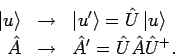
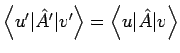 . Wenn
. Wenn ![\begin{eqnarray*}
\delta \left\vert u\right\rangle &=&i\varepsilon \hat{F}\left\...
...e ,
\\
\delta A &=&i\varepsilon \left[ \hat{F},\hat{A}\right] .
\end{eqnarray*}](img1777.png)