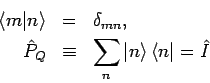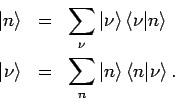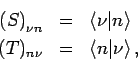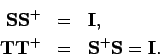Next: Einige Darstellungen
Up: Formalismus der Quantenmechanik und
Previous: Unitäre Transformationen.
Contents
Darstellungen der Quantenmechanik
Betrachten wir den Hilbert-Raum 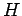 , und darin ein VONS der Basisvektoren
, und darin ein VONS der Basisvektoren
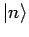 . Wenn
. Wenn
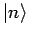 Eigenvektoren
irgendeiner Observablen
Eigenvektoren
irgendeiner Observablen 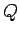 sind,
sind,
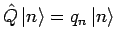 , sagen wir, dass
, sagen wir, dass
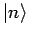 die Basisvektoren
in
die Basisvektoren
in 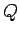 -Darstellung sind. Es gilt:
-Darstellung sind. Es gilt:
Die Basisvektoren einer Darstellung können über die Basisvektoren
einer anderen Darstellung
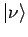 (VONS der
Eigenfunktionen einer Observablen
(VONS der
Eigenfunktionen einer Observablen 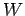 ) entwickelt werden:
) entwickelt werden:
Die Skalarprodukte, die von den beiden Darstellungen abhängen,
können als Elemente einer Matrix aufgefasst werden:
es gilt
(Die Matrizen 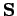 und
und 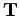 sind nicht unbedingt
quadratisch, da im Prinzip die Anzahl der Basisvektoren in verschiedenen
Darstellungen unterschiedlich sein kann, oder einer der Operatoren kann ein
kontinuierliches Spektrum haben, wobei der andere ein diskretes Spektrum
besitzt). Es gilt:
sind nicht unbedingt
quadratisch, da im Prinzip die Anzahl der Basisvektoren in verschiedenen
Darstellungen unterschiedlich sein kann, oder einer der Operatoren kann ein
kontinuierliches Spektrum haben, wobei der andere ein diskretes Spektrum
besitzt). Es gilt:
Wenn ein Operator  in
in 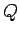 -Darstellung durch eine Matrix
-Darstellung durch eine Matrix
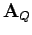 dargestellt wird, so wird er in
dargestellt wird, so wird er in 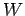 -Darstellung durch eine Matrix
-Darstellung durch eine Matrix
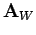 dargestellt, mit Matrizenelementen
dargestellt, mit Matrizenelementen
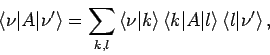 |
(43) |
d.h.
Analog, für die rechten Vektoren
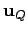 und
und
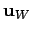 die in beiden Darstellungen das gleichen Ket
die in beiden Darstellungen das gleichen Ket
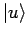 repräsentieren gilt
repräsentieren gilt
da
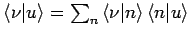 , für die linke Vektoren
, für die linke Vektoren
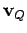 und
und
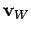 , die dem Bra
, die dem Bra
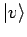 entsprechen, gilt
entsprechen, gilt
Die Lösung des Eigenwertproblems für Operator 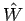 in
in 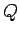 -Darstellung ist äquivalent zu der Suche nach der Transformation
-Darstellung ist äquivalent zu der Suche nach der Transformation 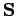 , die
, die 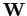 diagonalisiert. Umgekehrt, die Lösung der
Eigenwertproblem für Operator
diagonalisiert. Umgekehrt, die Lösung der
Eigenwertproblem für Operator 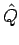 in
in 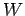 -Darstellung ist
äquivalent zu der Suche nach der Transformation
-Darstellung ist
äquivalent zu der Suche nach der Transformation
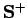 , die
, die 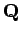 diagonalisiert.
diagonalisiert.
Subsections




Next: Einige Darstellungen
Up: Formalismus der Quantenmechanik und
Previous: Unitäre Transformationen.
Contents
Prof. Igor Sokolov
2005-02-14
![]() , und darin ein VONS der Basisvektoren
, und darin ein VONS der Basisvektoren
![]() . Wenn
. Wenn
![]() Eigenvektoren
irgendeiner Observablen
Eigenvektoren
irgendeiner Observablen ![]() sind,
sind,
![]() , sagen wir, dass
, sagen wir, dass
![]() die Basisvektoren
in
die Basisvektoren
in ![]() -Darstellung sind. Es gilt:
-Darstellung sind. Es gilt: