Schrödinger-Bild.

Falls sich das Spektrum des Operators zeitlich nicht ändert, kann man die Operatoren verwenden, deren Form zeitunabhängig ist. Die zeitliche Änderung des Zustandes wird in diesem Fall durch die Änderung (Drehung) des Zustandsvektors bestimmt. Im Schrödinger-Bild wird die zeitliche Änderung der Wellenfunktion durch die Schrödinger-Gl. festgelegt.

Die Zeitabhängigkeit der WF in Schrödinger-Bild kann symbolisch mit Hilfe der unitären Transformation

$$\psi (x,t)=\hat{S}(t)\psi (x,0)$$

dargestellt werden. Die Unitärität $\hat{S}^{+}(t)\hat{S}(t)=\hat{I}$ ist notwendig, damit die Normierung der WF erhalten bleibt. Stellen wir den Ausdruck für $\psi (x,t)$ in der Schrödinger-Gl. ein, so erhalten wir

$$\left[ i\hbar \frac{\partial }{\partial t}\hat{S}(t)-\hat{H}\hat{S}% (t)\right] \psi (x,0)=0.$$

Das entspricht einer Operatorbeziehung

$$i\hbar \frac{\partial }{\partial t}\hat{S}(t)-\hat{H}\hat{S}(t)=0.$$

Falls $\hat{H}$ nicht explizit von $t$ abhängt, ergibt sich die formale Lösung

$$\hat{S}(t)=\exp \left( -\frac{i}{\hbar }\hat{H}t\right)$$

(Anfangsbedingung $\hat{S}(0)=\hat{I}$). Die zeitliche Änderung des Zustandes wird also durch

$$\psi (x,t)=\exp \left( - \frac{i}{\hbar }\hat{H}t\right) \psi (x,0)$$

gegeben.

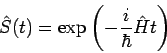
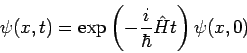
Um die Situation klarer zu machen, entwickeln wir die WF nach Eigenfunktionen von $\hat{H}$:

$$\begin{eqnarray*} \psi (x,t) &=&\sum_{k}\frac{1}{k!}\left(- \frac{i}{\hbar }\hat... ...{n}c_{n}\exp \left(- \frac{i}{\hbar }E_{n}t\right) \psi _{n}(x). \end{eqnarray*}$$

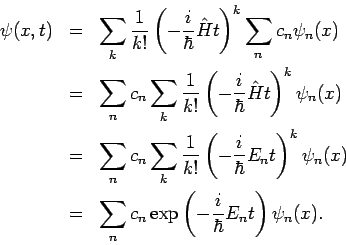
Man könnte auch sofort in der Energiedarstellung (in der $\hat{H}$ diagonal ist) schreiben

$$\exp \left( -\frac{i}{\hbar }\hat{H}t\right) \psi (E_{n})=\exp \left(- \frac {i}{\hbar }E_{n}t\right) \psi (E_{n})$$

(das ist die Definition einer Funktion eines Operators!) und dann zur Ortsdarstellung zurückkehren.

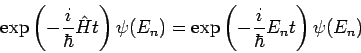
Die Wellemechanik, womit wir den ersten Teil dieses Kurses uns beschäftigt hatten, entspricht der Benutzung des Schrödinger-Bildes und der Ortsdarstellung.