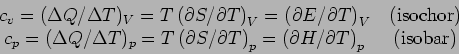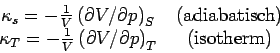Wichtigste Begriffe der Thermodynamik

$\bullet$ Beobachtung: Existenz des thermodynamischen Gleichgewichtszustandes (GG)

$\bullet$ Die Hauptsätze:

0. Zwei Systeme, die sich im GG mit einem dritten System befinden, sind auch untereinander im GG. Folgerung: $\exists$ $T$ (Temperatur als intensive Zustandsfunktion).

1. $dE=\delta Q+\delta A$

2. Es ist unmöglich, eine periodisch funktionierende Maschine zu konstruieren, die weiter nichts bewirkt, als Verrichtung von Arbeit und Wärmeabnahme aus einem Wärmereservoir.

Gleichwertige Formulierung: $\exists$ $S$ (Entropie als extensive Zustandsfunktion, $S(E,V,N...)$): $dS\geq \delta Q/T$.

$\bullet$ Reversible Prozesse: $dS=\delta Q/T$ $\Longrightarrow$

$dE\underbrace{(S,V,N,...)}$	$=TdS-pdV+\mu \delta N$	+ $\underbrace{...}$
Alle natürliche		$HdM$ für magn. Systeme
Variablen von $E$		$EdP$ für dielektrische Syst.
sind extensiv

mit

$$\begin{eqnarray*} &&T\mbox{ - Temperatur} \\ &&S\mbox{ - Entropie} \\ &&p\mbox... ...\mu \mbox{ - chemisches Potential} \\ &&N\mbox{ - Teilchenzahl} \end{eqnarray*}$$

$\bullet$ Temperatur:

$$\frac{1}{T}=\frac{\partial S(E,V,N...)}{\partial E}$$

$\bullet$ Im Gleichgewicht 2 Systeme:

$$\begin{tabular}{\vert\vert p{1in}\vert\vert p{1in}\vert\vert} \hline\hline 1 & 2 \\ \hline\hline \end{tabular}$$

$$\begin{eqnarray*} T_{1} &=&T_{2} \\ p_{1} &=&p_{2} \\ \mu _{1} &=&\mu _{2} \end{eqnarray*}$$

$\bullet$ TD Potentiale und ihre natürlichen Variablen:

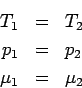
TD Potentiale sind Funktionen ihrer natürlichen Variablen d.h. es sind vollständige Differentiale:

$$\begin{array}{llll} \underline{Potential} & \underline{Bezei... ... T.V,\mu & d\Omega =-SdT-pdV-Nd\mu +...\\ &=-pV && \end{array}$$

$\bullet$ Die wichtigsten abgeleiteten Größen:

Die spezifische Wärme

$$\begin{tabular}{cc} $c_{v}=(\Delta Q/\Delta T)_{V}=T\left( \... ... \partial H/\partial T\right) _{p}$\ & (isobar) \end{tabular}$$

Kompressibilität

$$\begin{tabular}{cc} $\kappa _{s}=-\frac{1}{V}\left( \partial... ...\partial V/\partial p\right) _{T}$\ & (isotherm) \end{tabular}$$

Ausdehnungskoeffizient (isobar)

$$\alpha =\frac{1}{V}\left( \partial V/\partial T\right) _{p}$$

Magnetische Suszeptibilität

$$\chi =\left( \partial M/\partial H\right) _{T}.$$

Diese Größen können durch die verschiedenen zweiten partiellen Ableitungen der TD Potentiale ausgedrückt werden.