Statistische Gesamtheiten

$\bullet$ Vergröberte Beschreibung: Mikrozustände $% \rightarrow$ Makrozustand, charakterisiert durch größte Unkenntnis. Beschreibung durch die Informationsfunktion

$$S=-k \sum_{i}w_{i} \ln w_{i}$$ (1)

($w_{i}$- Wahrscheinlichkeit des Mikrozustandes $i$ ( $\sum_{i}w_{i}=1$) ) wird als statistisches Gegenstück zur thermodynamischen Entropie betrachtet; $k=1.380658\cdot 10^{-23}$ J/K ist die Boltzmann-Konstante.

Beschreibung im Rahmen der Theorie der statistischen Gesamtheiten

$\bullet$ Die drei wichtigsten Gesamtheiten der Statistischen Physik:

$\blacktriangleright$ Mikrokanonosche Gesamtheit (abgeschlossene Systeme): Alle Mikrozustände sind gleichwahrscheinlich (Spezialfall der kanonischen gesamtheit).

$\blacktriangleright$ Kanonische Gesamtheit (Systeme im Kontakt mit einem Wärmebad); $E_{i}$ variabel, die mittlere Energie

$$E=\sum_{i}E_{i}w_{i}$$ (2)

ist identisch mit der inneren Energie.

Die Gibbs-Verteilung: Maximierung von $S$, Eq.(1), unter den Nebenbedingung (25) ergibt

$$w_{i}=\frac{1}{Z_{k}}e^{-\beta E_{i}}$$ (3)

wobei $\beta$ ein Lagrange'scher Multiplikator ist. Die physikalische Bedeutung von $\beta$:

$$\beta =\frac{1}{kT}$$

(inverse Temperatur in Einheiten der Energie). Der Nenner von (26)

$$Z_{K}=\sum_{i}e^{-\beta E_{i}}$$

ist die kanonische Zustandssumme. Wichtigste Beziehung

$$\fbox{$F(T,V,N)=-kT\ln Z_{K} (T,V,N).$}$$

Somit ist die praktische Aufgabe der statistischen Physik die Berechnung der Zustandssummen.

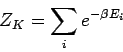
Bemerkung: Die mikrokanonische Gesamtheit kann als Spezialfall der kanonischen mit $E_{i}=E$ und somit mit gleichen Wahrscheinlichkeiten $% w_{i}$ betrachtet werden.

$\blacktriangleright$ Großkanonische Gesamtheit (Systeme im Kontakt mit einem Wärmebad; Teilchenaustausch mit der Umgebung ist möglich); die Mikrozustände sind durch variable $E_{i}$ und $N_{i}$ gegeben. Maximierung von $S$ unter den Nebenbedingungen (25) und

$$N=\sum_{i}N_{i}w_{i}$$

ergibt

$$w_{i}=\frac{1}{Z_{g}}e^{-\beta E_{i}-\gamma N_{i}}.$$

Die Lagrange'schen Multiplikatoren sind

$$\beta =\frac{1}{kT}\mbox{ und }\gamma =-\frac{\mu }{kT}.$$

Somit hat man

$$Z_{G}=Z(T,V,\mu )=\sum_{i}e^{\frac{\mu N_{i}-E_{i}}{kT}}.$$

Wichtigste Beziehung:

$$\fbox{$\Omega (T,V,\mu )=-kT\ln Z_{G} (T,V,\mu )$}$$

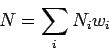
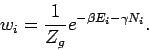
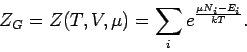
$\bullet$ Die Möglichkeit der statistischen Beschreibung basiert auf einem Postulat, wonach Zeit- und die Scharmittel für thermodynamische Systeme identisch sind (Ergodenhypothese).