


Nächste Seite: Kanonische Verteilung aus der
Aufwärts: Die Mikrokanonische Gesamtheit
Vorherige Seite: Die Mikrokanonische Gesamtheit
 Energie fest
Energie fest 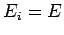
 Gesamtzahl der Realisierungen
Gesamtzahl der Realisierungen 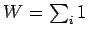
 Zustandssumme
Zustandssumme
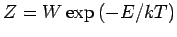
 Entropie
Entropie 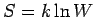
Übergang zur Kontinuum:
Typischerweise betrachtet man die Zustände in einem kleinen
Energieintervall
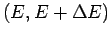 . Die Anzahl dieser Zustände ist
. Die Anzahl dieser Zustände ist
wobei 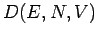 die Zustandsdichte ist.
die Zustandsdichte ist.
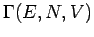 stellt das
Volumen im Phasenraum dar, das allen Zuständen
stellt das
Volumen im Phasenraum dar, das allen Zuständen 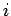 mit
mit 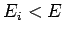 zu
Verfügung steht (Anzahl aller Zustände mit
zu
Verfügung steht (Anzahl aller Zustände mit 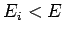 ).
).
Übergang zur Kontinuum, nicht-unterscheidbare Teilchen,
Speziallfall: ideales Gas,
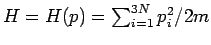 .
.
Sei
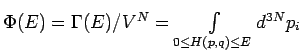 ,
dann ist
,
dann ist
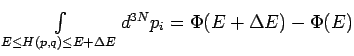 . Für ein ideales Gas ist
. Für ein ideales Gas ist 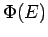 das Volumen
einer
das Volumen
einer 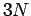 -dimensionalen Kugel im Impulsraum mit Radius
-dimensionalen Kugel im Impulsraum mit Radius
 . Der mathematische Ausdruck
für das Volumen einer
. Der mathematische Ausdruck
für das Volumen einer 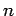 -dimensionalen Kugel ist
-dimensionalen Kugel ist
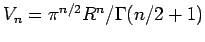 . Unter Benutzung der Stirling-Formel erhalten
wir
. Unter Benutzung der Stirling-Formel erhalten
wir
Nochmalige Benutzung der Stirling-Formel ergibt dann
Daraus folgt schlie▀lich:
(die Sakur-Tetrode-Gleichung).
Prof. Igor Sokolov
2004-07-01
![]() Energie fest
Energie fest ![]()
![]() Gesamtzahl der Realisierungen
Gesamtzahl der Realisierungen ![]()
![]() Zustandssumme
Zustandssumme
![]()
![]() Entropie
Entropie ![]()
![]() . Die Anzahl dieser Zustände ist
. Die Anzahl dieser Zustände ist
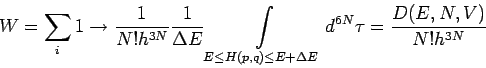
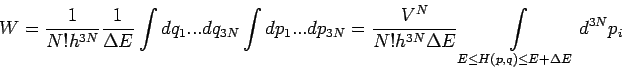
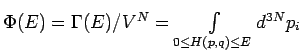 ,
dann ist
,
dann ist
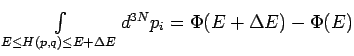 . Für ein ideales Gas ist
. Für ein ideales Gas ist 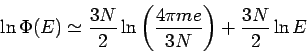
![\begin{displaymath}
W(E,V,N)=\frac{V^{N}}{N!h^{3N}}\frac{d}{dE}\Phi (E)\simeq \...
...ft( \frac{4\pi mE}{3h^{2}N}\right) ^{3/2}e^{5/2}\right] ^{N}.
\end{displaymath}](img249.png)
![\begin{displaymath}
S(E,V,N)=k\ln W=kN\ln \left[ \frac{V}{N}\left( \frac{4\pi mE}{3h^{2}N}%
\right) ^{3/2}e^{5/2}\right]
\end{displaymath}](img250.png)