Die Mikrokanonische Gesamtheit

Aus statistischer Sicht liefert die mikrokanonische Gesamtheit nur einen Spezialfall der kanonischen Gesamtheit, in der alle Einzelsysteme die gleiche Energie und die gleichen Werte für Volumen und Teilchenzahl besitzen. Die ist aber prinzipiell wichtig, da hier die Anknüpfung der Statistische Physik an Mechanik erfolgt.

* Bemerkung: Sog. Molekulardynamische Simulationen (h.h. die numerische Lösung der Bewegungsgleichungen für ein ''mittelgrosses'' System der Teilchen (Moleküle) ( $N\sim 10^{3}-10^{6}$) bedient sich der mikrokanonischen Gesamtheit, und liefert i.d.R. die mechanischen Größen (z.B. Druck) und die Entropie als Funktionen der Energie des Systems, die durch die Anfangsbedingungen gegeben ist. Dagegen bedienen sich die sog. Monte-Carlo-Zugänge explizit mit der kanonischen Zusammenhänge.

Klassisch ist ein geschlossenes System von $N$ Teilchen durch ein Punkt $(q_{1},q_{2},...,q_{3N};p_{1},...,p_{3N})$ in $6N$-dimensionalen Phasenraum $\Gamma$ beschrieben. Zeitliche Änderungen werden durch eine Trajektorie im Phasenraum beschrieben. Für ein Hamilton-System

$$p_{i}=-\frac{\partial H}{\partial q_{i}};\qquad q_{i}=\frac{\partial H}{% \partial p_{i}}\qquad (i=1,2,...,3N)$$ (5)

($H$ ist die Hamilton-Fkt. des Systems). Eine Gesamtheit entspricht einer Menge der Punkten im Phasenraum. Beschreibung durch die Dichtefunktion (Verteilungsfunktion) $\rho (q_{1},q_{2},...,q_{3N};p_{1},...,p_{3N})=\rho (% \vec{q},\vec{p})$; die kann auch explicit von der Zeit abhängen: $\rho (% \vec{q},\vec{p},t)$.

$\bullet$ Der Liouvillesche Satz

$$\frac{d\rho }{dt}\equiv \frac{\partial \rho }{\partial t}+\... ...+\frac{\partial \rho }{\partial p_{i}}\dot{p}_{i}\right) =0$$

(die Verteilung der Systeme bewegt sich wie eine inkompressible Flüssigkeit durch den $\Gamma$-Raum; die Hamilton-Gl. (5) liefert die Inkompressibilitätsbedingung!).

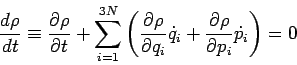
Folgerung: Phasenvolumina bleiben konstant während der zeitlichen Entwicklung.

Bedingungen für das Gleichgewicht: Im GG ändern sich die Mittelwerte (die alle als $\int f(\vec{q},\vec{p})\rho (\vec{q},\vec{p},t)d\vec{q}d\vec{p}$ ausgedruckt werden können) nicht. Hinreichende Bedingung dafür ist $\frac{\partial \rho }{\partial t}=0$, d.h. $\rho (% \vec{q},\vec{p},t)=\rho (\vec{q},\vec{p})$. Diese Bedingung wird erfüllt wenn $\rho (\vec{q},\vec{p})=\rho (A_{1}(\vec{q},\vec{p}),...,A_{n}(\vec{q},% \vec{p}))$, wobei $A_{1},...,A_{n}$ die Erhaltungsgrößen (Bewegungsintegrale) der Systeme der Gesamtheit sind. Eigentlich ist

$$\rho (\vec{q},\vec{p})=\rho (H(\vec{q},\vec{p}))$$

(für thermodynamische Systeme die als Ganzes ruhen).

Bemerkung: Unabhängig vom Anfangszustand, wird die Situation (GG) erreicht, in der Zustände mit gleicher Energie gleichwahrscheinlich sind $\Rightarrow$

Die im Phasenraum an die $H(\vec{q},\vec{p})=E$ -Hyperfläche gebundene Phasentrajektorie kommt im Laufe der Zeit jedem Punkt dieser Fläche beliebig nahe.

(Quasiergodenhypothese, P. & T. Ehrenfest, 1911).