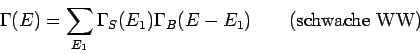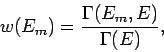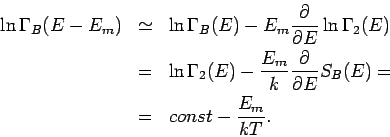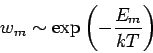Nächste Seite: Die Großkanonische Zustandssumme
Aufwärts: Die Mikrokanonische Gesamtheit
Vorherige Seite: Berechnung der Mikrokanonischen Zustandssumme
Wir betrachten 2 Systeme von sehr unterschiedlicher Größe, und mit
sehr schwacher Kopplung, das Wärmebad (das viel
größere System) und ''das System''. Beide zusammen bilden ein
abgeschlossenes System (''Gesamtsystem'') und werden im Rahmen einer
mikrokanonischen Gesamtheit beschrieben. Das Systems besitzt diskrete
Energieniveaus; die Energieniveaus des Wärmebades bilden
praktisch ein kontinuierliches Spektrum. Für das Gesamtsystem
(mit
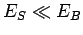 wegen dem Größenunterschied) und
wegen dem Größenunterschied) und
(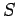 -''das System'',
-''das System'', 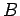 -Bad).
-Bad). 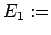 Alle mögliche Energien des
Systems. Das Fixieren des Zustandes
Alle mögliche Energien des
Systems. Das Fixieren des Zustandes 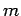 des Systems entspricht dann für
das Gesamtsystem dem Phasenvolumen
des Systems entspricht dann für
das Gesamtsystem dem Phasenvolumen
Die Wahrscheinlichkeit der Realisierung eines solchen Zustandes ist dann
da alle Zustände des Gesamtsystems mit Energie 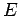 apriori
gleichwahrscheinlich sind. Da
apriori
gleichwahrscheinlich sind. Da

(kanonische Verteilung).
Prof. Igor Sokolov
2004-07-01