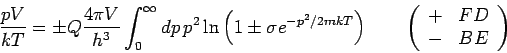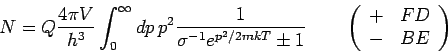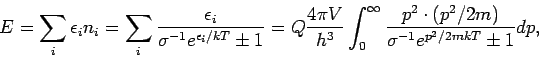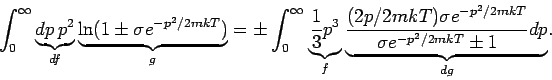Nächste Seite: Das ideale Fermi-Gas
Aufwärts: Exakte Statistik nichtwechselwirkender Teilchen
Vorherige Seite: Fermi-Dirac Statistic
Voraussetzung: nur Translationsfreiheitsgrade,
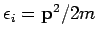 . Bezeichnung:
. Bezeichnung:
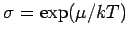 für die Fugazität. Die
allgemeinen Beziehungen lauten:
für die Fugazität. Die
allgemeinen Beziehungen lauten:
und
Berücksichtigung des Spins: In Abwesenheit eines Magnetfeldes gibt es für ein Teilchen mit Spin 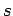
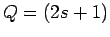 Einstellungsmöglichkeiten (
Einstellungsmöglichkeiten (
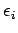 spinunabhängig). Daher: zusätzlicher Vorfaktor
Q.
spinunabhängig). Daher: zusätzlicher Vorfaktor
Q.
Übergang zum Kontinuum (in 3 Dimensionen) liefert (
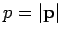 ):
):
Bemerkung: Wie für ein klassisches Idealgas gilt es für die idealen
Fermi- und Bose-Gase mit einem quadratischen Dispersionsgesetz (
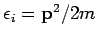 )
)
(für ein klassisches Gas 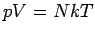 und
und
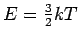 ).
).
Da
genügt es, durch die partielle Integration zu zeigen, dass
Damit folgt die Entropie
Um die thermischen Zustandsgleichungen für die entsprechende Gase zu
be/-stimmen, d.h. um 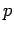 als Funktion von
als Funktion von 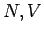 und
und 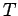 auszudrucken, muß man die Fugazität aus der Gleichungen für
auszudrucken, muß man die Fugazität aus der Gleichungen für 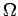 und
und 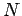 eliminieren.
eliminieren.
Unterabschnitte



Nächste Seite: Das ideale Fermi-Gas
Aufwärts: Exakte Statistik nichtwechselwirkender Teilchen
Vorherige Seite: Fermi-Dirac Statistic
Prof. Igor Sokolov
2004-07-01
![]() . Bezeichnung:
. Bezeichnung:
![]() für die Fugazität. Die
allgemeinen Beziehungen lauten:
für die Fugazität. Die
allgemeinen Beziehungen lauten:
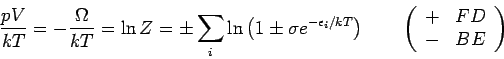
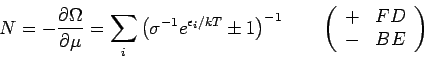
![]() ):
):