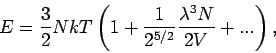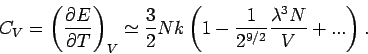Nächste Seite: Maximale Entartung ()
Aufwärts: Das ideale Fermi-Gas
Vorherige Seite: Das ideale Fermi-Gas
Das Verhalten ähnelt einem klassischen Gas, 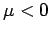 .
.

Damit folgt
und
(Entwicklung nach Potenzen von 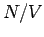 , Virialentwicklung).
, Virialentwicklung).
Prof. Igor Sokolov
2004-07-01
![]() .
.
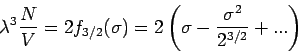
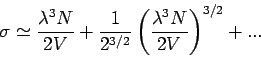
![\begin{displaymath}
\mu =kT\ln \sigma \simeq kT\left[ \ln \left( \frac{\lambda ^...
...\frac{1}{2}\left( \frac{\lambda ^{3}N}{2V}\right) +...\right]
\end{displaymath}](img352.png)