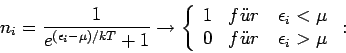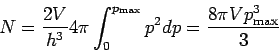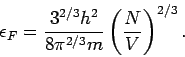Nächste Seite: Starke Entartung,
Aufwärts: Das ideale Fermi-Gas
Vorherige Seite: Schwache Entartung ()
Für
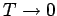
Alle Einteilchenzustände unterhalb
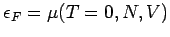 sind
besetzt, alle höher liegende Zustände sind leer.
sind
besetzt, alle höher liegende Zustände sind leer. 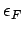 :
die Fermi-Energie.
:
die Fermi-Energie.
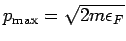 .
.

Bemerkung:
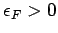 und
und
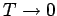 entspricht die
Situation
entspricht die
Situation
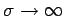 .
.
Prof. Igor Sokolov
2004-07-01
![]()