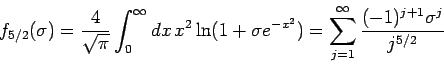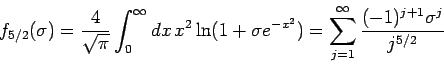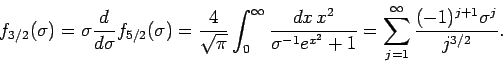Nächste Seite: Schwache Entartung ()
Aufwärts: Die Ideale Bose- und
Vorherige Seite: Die Ideale Bose- und
Führen wir die zwei Hilfsfunktionen ein:
und
Ausgedruckt durch diese Funktionen ergibt sich
und
(
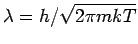 die thermische Wellenlänge; es wird
angenommen
die thermische Wellenlänge; es wird
angenommen 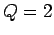 ). Geschlossene analytische Formen der
Zustandsgleichungen gibt es nur als Näherungen für Spezialfälle.
). Geschlossene analytische Formen der
Zustandsgleichungen gibt es nur als Näherungen für Spezialfälle.
Unterabschnitte
Prof. Igor Sokolov
2004-07-01