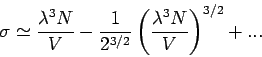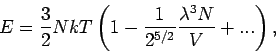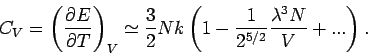Schwache Entartung ($\sigma <1$)

Das Verhalten ähnelt einem klassischen Gas, 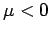$\mu <0$.

$$\lambda ^{3}\frac{N}{V}=g_{3/2}(\sigma )=\sigma +\frac{\sigma ^{2}}{2^{3/2}}% +...$$

$\Rightarrow$

$$\sigma \simeq \frac{\lambda ^{3}N}{V}-\frac{1}{2^{3/2}}\left( \frac{\lambda ^{3}N}{V}\right) ^{3/2}+...$$

Damit folgt

$$\frac{pV}{NkT}=\frac{V}{\lambda ^{3}N}g_{5/2}(\sigma )\simeq 1-\frac{1}{% 2^{5/2}}\frac{\lambda ^{3}N}{V}+...,$$

$$E=\frac{3}{2}NkT\left( 1-\frac{1}{2^{5/2}}\frac{\lambda ^{3}N}{V}+...\right) ,$$

und

$$C_{V}=\left( \frac{\partial E}{\partial T}\right) _{V}\simeq... ...\left( 1-\frac{1}{2^{5/2}}\frac{\lambda ^{3}N}{V}+...\right) .$$

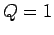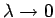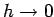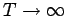(Andere Vorzeichen als bei einem Fermi-Gas, andere Vorfaktor wegen den angenommenen $Q=1$). Somit bekommt man für $\lambda \rightarrow 0$ ( $% h\rightarrow 0$ oder $T\rightarrow \infty$) die klassische Ergebnisse.