


Nächste Seite: Photonen und Phononen
Aufwärts: Das ideale Bose-Gas
Vorherige Seite: Schwache Entartung ()
Wir wissen bereits, dass für ein System von Bosonen 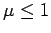 und
deswegen
und
deswegen 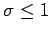 .
.
Mit
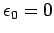 divergiert der Summand für
divergiert der Summand für 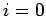 wenn
wenn
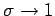 . Der muß dann bei der Übergang zur Kontinuum getrennt
berücksichtigt werden, da es sonst das Gewicht
. Der muß dann bei der Übergang zur Kontinuum getrennt
berücksichtigt werden, da es sonst das Gewicht 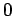 (wegen
(wegen 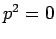 )
bekommt; mit allen anderen Glieder können wir wie gewohnt umgehen.
)
bekommt; mit allen anderen Glieder können wir wie gewohnt umgehen.

Das erste Glied 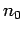 ist die mittlere Teilchenzahl im Grundzustand
(neues Glied!). Für
ist die mittlere Teilchenzahl im Grundzustand
(neues Glied!). Für 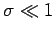 ist
ist 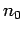 vernachlässigbar,
divergiert aber wenn
vernachlässigbar,
divergiert aber wenn
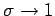 ).
).
Es gilt:
(um das zu sehen merkt man dass
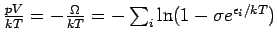 , mit
, mit
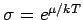 und dass
und dass 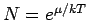 ).
). 
Es ist wichtig, dass die Funktionen
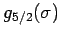 und
und
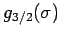 stetig in 1 sind:
stetig in 1 sind:
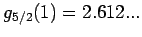 und
und
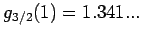 .
.
Die Funktionen
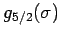 und
und
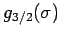 sind monoton
wachsend im Intervall
sind monoton
wachsend im Intervall
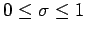 .
.
 Maximaler Wert von
Maximaler Wert von
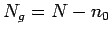 ist
ist
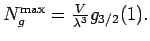 Bei
vorgegebenem Wert von
Bei
vorgegebenem Wert von 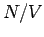 gibt es eine Grenztemperatur
gibt es eine Grenztemperatur
so dass für 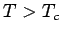 und für
und für
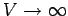 (bei der
konstante Dichte
(bei der
konstante Dichte 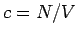 )
)
und für 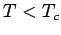
Dieser Effekt wird als Bose-Einstein-Kondensation bezeichnet.
Die Energie im Grundzustand ist null, so dass
was im kontinuierlichen Fall liefert

Der Druck lautet
Damit ist der Druck für 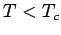 nur noch von der Temperatur und nicht
von dem Volumen abhängig: Die Volumenänderung bei konstanter
nur noch von der Temperatur und nicht
von dem Volumen abhängig: Die Volumenänderung bei konstanter 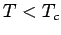 ändert nur die Anzahl der Bosonen im Grundzustand (die, mit
ändert nur die Anzahl der Bosonen im Grundzustand (die, mit 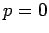 , nicht zum Druck beitragen können). Für
, nicht zum Druck beitragen können). Für 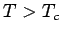 hängt der
Druck von
hängt der
Druck von 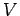 ab, da
ab, da 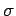 implizit von
implizit von 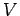 abhängig ist.
abhängig ist.
Die Bose-Einstein-Kondensation ist mit einer cusp-artigen Singularität
der spezifische Wärme verbunden: Die spezifische Wärme ist
kontinuierlich, ihre Ableitung nach 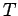 erleidet einen Sprung.
erleidet einen Sprung.
Die spezifische Wärme in der Tieftemperaturphase (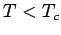 ) ist:
) ist:
Die Entropie lautet:
Für
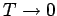 haben wir
haben wir
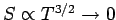 , was im
Einklang mit dem 3. Hauptsatz ist.
, was im
Einklang mit dem 3. Hauptsatz ist.
Bemerkung: Die Bose-Einstein-Kondensation (BEK) verdünnter
Gase (Alkali-Atome) wurde experimentell beobachtet: Nobelpreis 2001 für Eric Cornell, Wolfgang Ketterle und Carl Wiemann (Physics Today 54
(12), Dec. 2001 p.14). Die Suprafluidität des He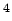 II ist ein
komplexeres Phänomen, da es in einem stark wechselwirkenden System (Flüssigkeit) stattfindet: Der
II ist ein
komplexeres Phänomen, da es in einem stark wechselwirkenden System (Flüssigkeit) stattfindet: Der 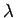 -Übergang findet bei
-Übergang findet bei 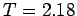 K
statt, ohne Berücksichtigung der WW wäre
K
statt, ohne Berücksichtigung der WW wäre 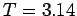 K. Die
Suprafluidität des He
K. Die
Suprafluidität des He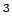 ist durch einfache BEK unerklärlich.
ist durch einfache BEK unerklärlich.



Nächste Seite: Photonen und Phononen
Aufwärts: Das ideale Bose-Gas
Vorherige Seite: Schwache Entartung ()
Prof. Igor Sokolov
2004-07-01
![]() und
deswegen
und
deswegen ![]() .
.
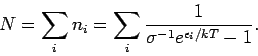
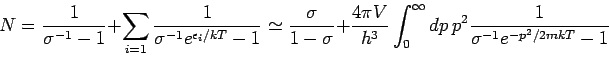
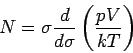
![]() und
und
![]() sind monoton
wachsend im Intervall
sind monoton
wachsend im Intervall
![]() .
.
![]() Maximaler Wert von
Maximaler Wert von
![]() ist
ist
![]() Bei
vorgegebenem Wert von
Bei
vorgegebenem Wert von ![]() gibt es eine Grenztemperatur
gibt es eine Grenztemperatur
![\begin{displaymath}
T_{c}=\frac{h^{2}}{2\pi mk}\left[ \frac{N}{Vg_{3/2}(1)}\right]
\end{displaymath}](img413.png)
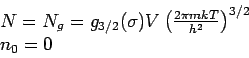
![\begin{displaymath}
\begin{array}{l}
N_{g}=g_{3/2}(1)V\left( \frac{2\pi mkT}{h^{...
...ft[ 1-\left( \frac{T}{T_{c}}\right) ^{3/2}\right] .
\end{array}\end{displaymath}](img419.png)
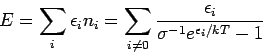
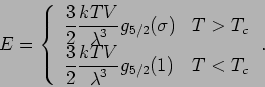
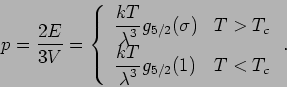
![]() erleidet einen Sprung.
erleidet einen Sprung.
![]() ) ist:
) ist:
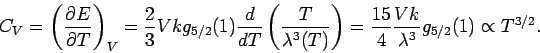
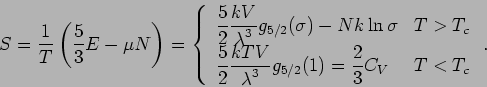
![]() II ist ein
komplexeres Phänomen, da es in einem stark wechselwirkenden System (Flüssigkeit) stattfindet: Der
II ist ein
komplexeres Phänomen, da es in einem stark wechselwirkenden System (Flüssigkeit) stattfindet: Der ![]() -Übergang findet bei
-Übergang findet bei ![]() K
statt, ohne Berücksichtigung der WW wäre
K
statt, ohne Berücksichtigung der WW wäre ![]() K. Die
Suprafluidität des He
K. Die
Suprafluidität des He![]() ist durch einfache BEK unerklärlich.
ist durch einfache BEK unerklärlich.