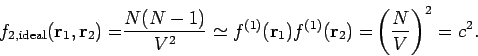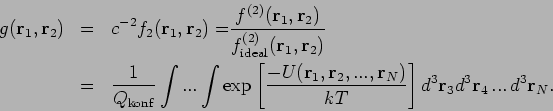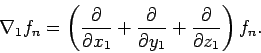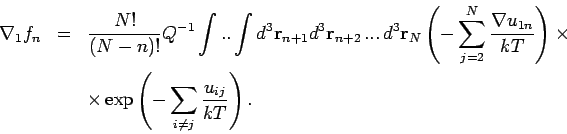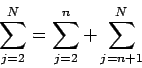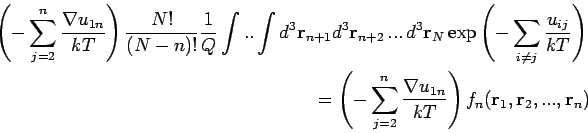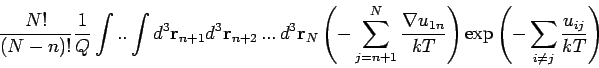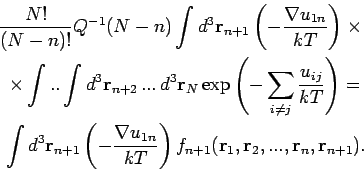Nächste Seite: Die BGY-Gleichung
Aufwärts: Statistische Theorie dichter Fluide
Vorherige Seite: Die Kompressibilitätsgleichung
Das ganze System aus 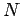 Teilchen, kanonisch betrachtet, wird durch die
folgende Wahrscheinlichkeitsverteilung aller Impulse und Koordinaten
charakterisiert:
Teilchen, kanonisch betrachtet, wird durch die
folgende Wahrscheinlichkeitsverteilung aller Impulse und Koordinaten
charakterisiert:
(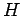 ist die Hamilton-Funktion, d.h. die Energie,
ist die Hamilton-Funktion, d.h. die Energie,
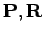 ist der Satz aller Impulse und Koordinaten). Integrieren über alle
Impluse (Gleichverteilung!) ergibt:
ist der Satz aller Impulse und Koordinaten). Integrieren über alle
Impluse (Gleichverteilung!) ergibt:
(siehe Kap. 3). Die allgemeine Verteilung 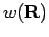 gibt uns die
Möglichkeit, die marginalen Verteilungen zu bilden.
gibt uns die
Möglichkeit, die marginalen Verteilungen zu bilden.
Zum Beispiel, gilt in einem homogenen System
Für ein Idealgas
Im Allgemeinen hat man
Differenzieren wir
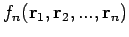 nach Koordinaten des ersten Teilchens. Bezeichnung:
nach Koordinaten des ersten Teilchens. Bezeichnung:
Die erste Summe wird in zwei geteilt
so dass der erste Teil ergibt
(über die Koordinaten
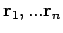 wird nicht
integriert). Der 2. Teil lautet
wird nicht
integriert). Der 2. Teil lautet
Das ist eine Summe von 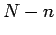 gleicher Glieder, da
gleicher Glieder, da
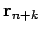 die
stumme Integrationsvariablen sind. Dieser Teil ist also
die
stumme Integrationsvariablen sind. Dieser Teil ist also
Sammeln wir jetzt alle Glieder:
Die Gl.(18) bilden eine unendliche Hierarchie der Gleichungen (YVON, 1935).



Nächste Seite: Die BGY-Gleichung
Aufwärts: Statistische Theorie dichter Fluide
Vorherige Seite: Die Kompressibilitätsgleichung
Prof. Igor Sokolov
2004-07-01
![]() Teilchen, kanonisch betrachtet, wird durch die
folgende Wahrscheinlichkeitsverteilung aller Impulse und Koordinaten
charakterisiert:
Teilchen, kanonisch betrachtet, wird durch die
folgende Wahrscheinlichkeitsverteilung aller Impulse und Koordinaten
charakterisiert:
![\begin{displaymath}
f(\mathbf{R})=\frac{\exp \left[ -U(\mathbf{R)/}kT\right] }{Q_{\rm konfig}}
\end{displaymath}](img653.png)
![\begin{eqnarray*}
&&f_{n}(\mathbf{r}_{1}\mathbf{r}_{2}...\mathbf{r}_{n})= \\
&&...
...] }{\int d^{3N}\mathbf{q}\exp \left[ -U(\mathbf{q)/}kT\right] }.
\end{eqnarray*}](img655.png)