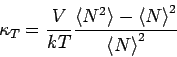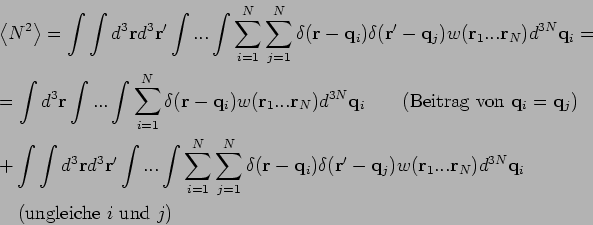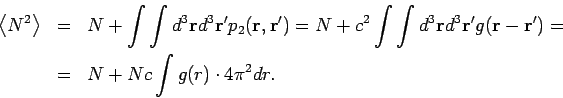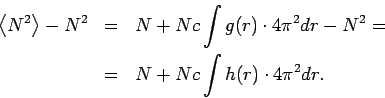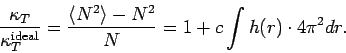Nächste Seite: Verallgemeinerte Verteilungsfunktionen.
Aufwärts: Die Paarverteilungsfunktion und die
Vorherige Seite: Die Druckgleichung
Die isothermische Kompressibilität eines Fluids
Für ein Idealgas gilt
Somit
Allgemeine Betrachtung der Dichteschwankungen: Wie bereits bewiesen, gilt:
Aus der Thermodynamik folgt:
Hier ist die Herleitung des thermodynamischen Beziehung:
Darüberhinaus gilt eine Maxwell-Beziehung (folgt aus 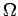 ):
):
Da 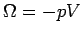 eine extensive Größe ist, gilt
eine extensive Größe ist, gilt
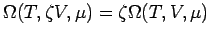 , das bedeutet, dass
, das bedeutet, dass
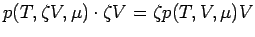 , so dass
, so dass 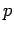 eigentlich volumenunabhängig
(oder Teichenzahlunabhängig) ist: in einem System mit vorgegebenem
eigentlich volumenunabhängig
(oder Teichenzahlunabhängig) ist: in einem System mit vorgegebenem 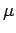 hängt der Druck nur von
hängt der Druck nur von 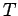 ab (vgl. Photonengas!). Bei vorgegebenen
Volumen stellt sich die Teilchenzahl so ein, dass
ab (vgl. Photonengas!). Bei vorgegebenen
Volumen stellt sich die Teilchenzahl so ein, dass
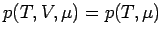 ; bei
vorgegebener mittleren Teilchenzahl stellt sich entsprechend das Volumen
ein! Also
; bei
vorgegebener mittleren Teilchenzahl stellt sich entsprechend das Volumen
ein! Also
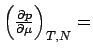
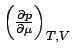 , das zweite Bedingung (
, das zweite Bedingung (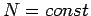 oder
oder 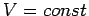 ist eigentlich redundant). Andere Herleitung siehe
BALESCU, Kap. 4.6.
ist eigentlich redundant). Andere Herleitung siehe
BALESCU, Kap. 4.6.
Weiterhin gilt

und
Nun gilt es:
Das erste Integral ist 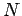 ; das zweite ist das Integral über die
Zweiteilchenverteilung:
; das zweite ist das Integral über die
Zweiteilchenverteilung:
Dann hat man
Daher ist
Das ist eine sehr elegante Formel die auch in der Theorie kritischer
Phänomene eine große Rolle spielt!



Nächste Seite: Verallgemeinerte Verteilungsfunktionen.
Aufwärts: Die Paarverteilungsfunktion und die
Vorherige Seite: Die Druckgleichung
Prof. Igor Sokolov
2004-07-01
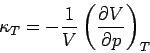
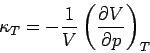
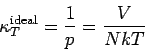
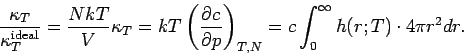
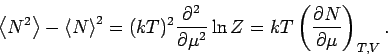
![\begin{displaymath}
\left( \frac{\partial N}{\partial \mu }\right) _{T,V}=-\left...
... \frac{\partial p}{\partial \mu }%
\right) _{T,V}\right] ^{2}
\end{displaymath}](img633.png)
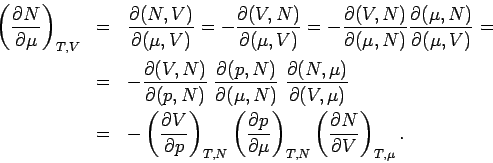
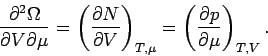
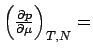
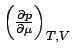 , das zweite Bedingung (
, das zweite Bedingung (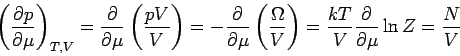
![\begin{displaymath}
\left( \frac{\partial N}{\partial \mu }\right) _{T,V}=-\left...
...al \mu }\right)
_{T,V}\right] ^{2}=\frac{\kappa _{T}}{V}N^{2}
\end{displaymath}](img645.png)