


Nächste Seite: Der Gleichverteilungssatz der Energie
Aufwärts: Die Kanonische Zustandssumme
Vorherige Seite: Die Kanonische Zustandssumme
Für ein klassisches System
wobei 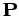 und
und 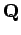 alle Impulse und Koordinaten des Systems
sind. Es gilt:
alle Impulse und Koordinaten des Systems
sind. Es gilt:

Der Ausdruck
hat die Dimension einer Länge. 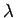 wird die thermische
Wellenlänge genannt und entspricht der de-Broglie-Wellenlänge bei
der Energie
wird die thermische
Wellenlänge genannt und entspricht der de-Broglie-Wellenlänge bei
der Energie 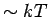 .
Das Integral
.
Das Integral  stellt die Zustandssumme im Konfigurationsraum dar.
Für die freie Energie ergibt sich
stellt die Zustandssumme im Konfigurationsraum dar.
Für die freie Energie ergibt sich
Wichtig: Das erste Beitrag hängt nicht von den geometrischen Bedingungen
des Systems ab, und trägt somit nicht zu den Kräften, Drucken, u.s.w.
bei. Daraus folgt
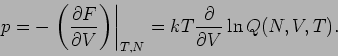 |
(4) |
Spezialfall athermische Systeme. Für viele recht
erfolgreiche Modelle nimmt man an, daß 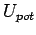 entweder verschwindet
oder unendlich ist. Z.B. ist für ein Idealgas
entweder verschwindet
oder unendlich ist. Z.B. ist für ein Idealgas 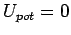 .
Wenn wir uns die Moleküle als harte Kugel vorstellen,
können wir annehmen, daß
.
Wenn wir uns die Moleküle als harte Kugel vorstellen,
können wir annehmen, daß
In diesem Fall gilt
und hängt damit nicht von 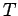 ab. Änliche Modelle bilden die
Standard-Modelle der Polymerphysik, u.s.w.
In diesem Fall ist
ab. Änliche Modelle bilden die
Standard-Modelle der Polymerphysik, u.s.w.
In diesem Fall ist
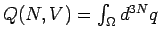 das gesamte zur Verfügung stehende Volumen des
das gesamte zur Verfügung stehende Volumen des 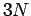 -dimensionalen
Konfigurationsraumes.
-dimensionalen
Konfigurationsraumes.
Bemerkung 1: In diesem Fall gilt, anhand der Gl.(4),
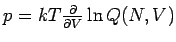 (linear in
(linear in 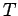 ).
Es wird oft gesagt,
das dieser Druck (oder die äquivalente thermodynamische Kraft) ist
von entropischer Natur.
).
Es wird oft gesagt,
das dieser Druck (oder die äquivalente thermodynamische Kraft) ist
von entropischer Natur.
Bemerkung 2: Wenn wir das Integral
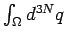 durch
eine Integralsumme annähern (was einer Diskretisierung des
Konfigurationsraums in Form einer Gitter mit Gitterkonstante
durch
eine Integralsumme annähern (was einer Diskretisierung des
Konfigurationsraums in Form einer Gitter mit Gitterkonstante 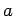 entspricht)
entspricht)
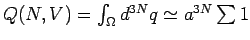 ,
wobei summiert wird über alle erlaubten Konfigurationen (
,
wobei summiert wird über alle erlaubten Konfigurationen (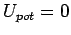 ).
Dann ergibt sich
).
Dann ergibt sich
wobei 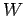 die Gesamtzahl der erlaubten Konfigurationen des Gittermodells ist.
Die entsprechenden Gittermodelle (Gitter-Gas, Random-Walk-Polymer, u.s.w.) sind
oft durch Anwendung der kombinatorischer Methoden lösbar, und sind
folglich höchst praktikabel zur Erklärung des Verhaltens realer
Stoffe.
die Gesamtzahl der erlaubten Konfigurationen des Gittermodells ist.
Die entsprechenden Gittermodelle (Gitter-Gas, Random-Walk-Polymer, u.s.w.) sind
oft durch Anwendung der kombinatorischer Methoden lösbar, und sind
folglich höchst praktikabel zur Erklärung des Verhaltens realer
Stoffe.



Nächste Seite: Der Gleichverteilungssatz der Energie
Aufwärts: Die Kanonische Zustandssumme
Vorherige Seite: Die Kanonische Zustandssumme
Prof. Igor Sokolov
2004-07-01
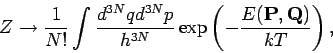
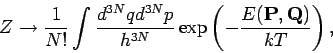
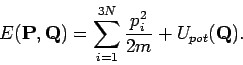
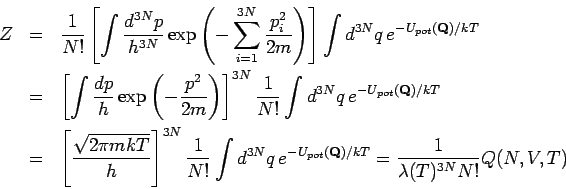
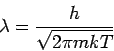
![\begin{eqnarray*}
F &=&-kT\ln Z= \\
&&-kT\left[ \frac{3}{2}N\ln \left( \frac{2\pi mkT}{h^{2}}\right) -\ln
N!\right] -kT\ln Q(N,V,T)
\end{eqnarray*}](img84.png)


![]() (linear in
(linear in ![]() ).
Es wird oft gesagt,
das dieser Druck (oder die äquivalente thermodynamische Kraft) ist
von entropischer Natur.
).
Es wird oft gesagt,
das dieser Druck (oder die äquivalente thermodynamische Kraft) ist
von entropischer Natur.
![]() durch
eine Integralsumme annähern (was einer Diskretisierung des
Konfigurationsraums in Form einer Gitter mit Gitterkonstante
durch
eine Integralsumme annähern (was einer Diskretisierung des
Konfigurationsraums in Form einer Gitter mit Gitterkonstante ![]() entspricht)
entspricht)
![]() ,
wobei summiert wird über alle erlaubten Konfigurationen (
,
wobei summiert wird über alle erlaubten Konfigurationen (![]() ).
Dann ergibt sich
).
Dann ergibt sich