Der Gleichverteilungssatz der Energie

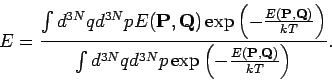
Wir berechnen kanonisch den Mittelwert der Energie. Es gilt

$$E=\frac{\int d^{3N}qd^{3N}pE(\mathbf{P},\mathbf{Q})\exp \le... ...\exp \left( -\frac{E(% \mathbf{P},\mathbf{Q})}{kT}\right) }.$$

Für $N$ nichtwechselwirkende Teilchen $E(\mathbf{P},\mathbf{Q}% )=\sum_{i=1}^{N}\epsilon _{i}(\vec{p}_{i},\vec{q}_{i})$. Dadurch

$$E=\sum_{i=1}^{N}\frac{\int d\vec{p}_{i}d\vec{q}_{i}\epsilon... ...\frac{\epsilon _{i}(\vec{% p}_{i},\vec{q}_{i})}{kT}\right) }$$

und für die identische Teilchen

$$E=N\frac{\int d\vec{p}d\vec{q}\epsilon (\vec{p},\vec{q})\ex... ...}\exp \left( -\frac{\epsilon (\vec{p},\vec{q})}{kT}\right) }$$

Sollten die Teilchen neben der Translation noch innere Freiheitsgrade besitzen (Vibration, Rotation) läßt sich analog mit insgesamt $g$ verallgemeinerte Koordinaten / Impulse formulieren

$$E=N\frac{\int dx_{1}...dx_{g}\epsilon (x_{1},...,x_{g})\exp... ...xp \left( -% \frac{\epsilon (x_{1},...,x_{g})}{kT}\right) }.$$

Falls $\epsilon$ separiert, i.e. $\epsilon =\epsilon _{f}(x_{1},...,x_{f})+\epsilon _{g}(x_{f+1},...,x_{g})$, folgt daß $E=E_{f}+E_{g}$. $E_{f}$ und $E_{g}$ sind durch Integrale integrale nur über die entsprechenden Koordinaten und Impulse gegeben.

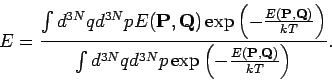
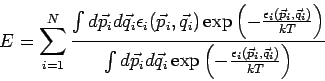
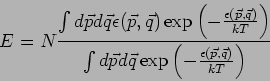
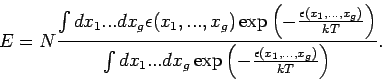
Seien nun nur diejenige Koordinaten und Impulse zum Satz $(x_{1},...,x_{f})$ zusammengefasst, die quadratisch in die Energie $\epsilon _{f}$ eingehen. (Beispiele: kinetische Energie freier Bewegung $\epsilon =p^{2}/2m$, harmonischer Oszillator, $U=m\omega ^{2}q^{2}/2m$, u.s.w. ). Dann liefert jede solche Variable den Beitrag $NkT/2$ zu $E$.

Beweis:

$$\epsilon _{f}(x_{1},...,x_{f})=\sum a_{i}x_{i}^{2}=\frac{1}... ...\frac{\partial \epsilon _{f}% }{\partial x_{f}}x_{f}\right)$$

Für das Integral im Zähler hat man

$$I=\frac{1}{2}\int e^{-\epsilon _{f}/kT}\left( \frac{\partial \eps... .....+\frac{\partial \epsilon _{f}}{\partial x_{f}}% x_{f}\right) dx_{1}...dx_{f}$$

$$=\frac{1}{2}\sum_{i=1}^{f}\int dx_{1}...dx_{f}e^{-\epsilon _{f}/kT}\frac{\partial \epsilon _{f}}{\partial x_{i}}x_{i}$$

Durch partielle Integration in $x_{i}$ bekommt man

$$\frac{1}{2}\sum_{i=1}^{N}\int dx_{1}...dx_{i}e^{-\epsilon _... ..._{i}=\frac{1}{2}kT\int e^{-\epsilon _{f}/kT}dx_{1}...dx_{f},$$

sodass $I=\frac{1}{2}fkT\int e^{-\epsilon _{f}/kT}dx_{1}...dx_{f}$ und

$$E_{f}=N\frac{I}{\int e^{-\epsilon _{f}/kT}dx_{1}...dx_{f}}=\frac{1}{2}NfkT.$$

Bemerkung: Das Gesetz gilt nur, wenn die Summe über die Zustände durch ein Integral ersetzt werden kann, d.h. nur im klassischen Fall bei höhere Tempreaturen.

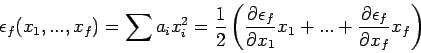
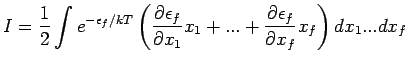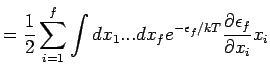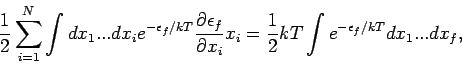
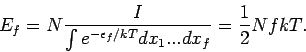
Anwendungsbeispiele:

$\bullet$ Einatomiges ideales Gas: $f=3$ (Nur Translation!) $% \Rightarrow$ $E=\frac{3}{2}NkT$. Die spezifische Wärmen: $c_{v}=\left( \frac{\partial E}{\partial T}\right) _{N,V}=\frac{3}{2}Nk$; $% c_{p}=c_{v}+T\left( \frac{\partial p}{\partial T}\right) _{N,V}\left( \frac{% \partial V}{\partial T}\right) _{N,p}=\frac{5}{2}Nk$

$\bullet$ Das zweiatomige ideale Gas (Modell: harte Hantel): $f=5$ $\Rightarrow$ $E=\frac{5}{2}NkT,$ $c_{v}=\frac{5}{2}Nk,$ $c_{p}=\frac{7}{2}% Nk$

$\bullet$ Dreiatomige Gase, starre asymmetrische Moleküle: $% f=6$ $\Rightarrow$ $E=3NkT,$ $c_{v}=3Nk$, $c_{p}=4Nk$.

Bemerkung: Die Betrachtung der molekularen Schwingungen erfordert i.d.R. quantenmechanischen Zugang.

$\bullet$ Der Festkörper als System von $N$ dreidimensionalen Oscillatoren; 6 Freiheitsgrade pro Atom (Einstein, 1907) $\Rightarrow$ Gesetz von Dulong-Petit. Aufgrund der Quanteneffekte gibt es viele Abweichungen auch bei moderaten Temperaturen (sieh unten).