Quantensysteme ![]() Diskrete Mikrozustände
Diskrete Mikrozustände ![]() Zustandssumme
Zustandssumme
Klassische Systeme ![]() Kontinuierliche Änderungen
Kontinuierliche Änderungen
![]() Zustandsintegral
Zustandsintegral
Mikrozustand ist charakterisiert durch ![]() Koordinaten
Koordinaten
![]() im Phasenraum. Zerlegung des Phasenraums
in Zellen, deren Größe eigentlich willkürlich gewält
werden kann.
Korrespondenz zur Quantenmechanik (Quasiklassisch:
1 Zustand pro
im Phasenraum. Zerlegung des Phasenraums
in Zellen, deren Größe eigentlich willkürlich gewält
werden kann.
Korrespondenz zur Quantenmechanik (Quasiklassisch:
1 Zustand pro ![]() ;
; ![]() - Plancksches Wirkungsquantum,
- Plancksches Wirkungsquantum,
![]() J
J![]() s):
s):
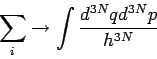
Wichtig: Ununterscheidbarkeit der Teilchen gleicher Sorte.
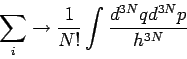
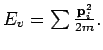
![\begin{displaymath}
Z=\frac{1}{N!}\frac{1}{h^{3N}}V^{N}\left[ \int dpe^{-p^{2}/2mkT}\right] ^{3N}
\end{displaymath}](img63.png)
Somit
![\begin{displaymath}
F=-kT\ln Z=-NkT\ln \left[ \frac{V}{N}e\left( \frac{2\pi mkT}{h^{2}}\right)
^{3/2}\right]
\end{displaymath}](img66.png)
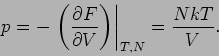
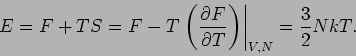
Die Entropie eines idealen Gases in ihren natürlichen Variablen ![]() und
und ![]() ist
ist
![\begin{displaymath}
S(E,V,N)=Nk\left\{ \ln \left[ \frac{V}{N}\left( \frac{4\pi m}{3h^{2}}\frac{E}{N}\right) ^{3/2}\right] +\frac{5}{2}\right\}
\end{displaymath}](img72.png)
Oft ist es notwendig, die Entropie als Funktion von ![]() ,
, ![]() und
und ![]() mittels
der thermischen Zustandsgleichungen auszudrucken. Hier ist den Ausdruck für die Entropie
mittels
der thermischen Zustandsgleichungen auszudrucken. Hier ist den Ausdruck für die Entropie
![\begin{displaymath}
\frac{S}{Nk}=-\ln p+\frac{5}{2}\ln T+\ln \left[ \left( \frac{2\pi m}{h^{2}}%
\right) ^{3/2}(ek)^{5/2}\right] .
\end{displaymath}](img74.png)