


Nächste Seite: Verhalten in ferromagnetischen Bereich
Aufwärts: Die Molekularfeldnäherung (Mean field
Vorherige Seite: Hilfsaufgabe: Freie Spins im
(am Beispiel des Ising-Modells).
Die Energie (''Hamilton-Funktion'') lautet
Idee: Wenigstens bei einem großen Zahl der Nachbarn kann man annehmen,
dass
mit 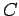 - Koordinationszahl (Anzahl der Nachbarn). Aus der Annahme von
Selbstkonsistenz
- Koordinationszahl (Anzahl der Nachbarn). Aus der Annahme von
Selbstkonsistenz
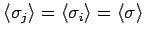 (
(
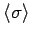 ist der Mittelwert des Spins im ganzen System). Dadurch
bekommt man als effektive Hamilton-Funktion
ist der Mittelwert des Spins im ganzen System). Dadurch
bekommt man als effektive Hamilton-Funktion
mit
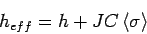 |
(21) |
dem Molekularfeld (mean field). Die Zustandssumme in solcher Näherung ist:
und
wie in dem Fall der nichtwechselwirkender Spins. Aus der Gl.(21) folgt
dann die Selbstkonsistenzbedingung
 Verhalten für
Verhalten für 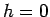 . Einführen
. Einführen
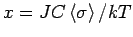 . Die Selbstkonsistenzgl. liest sich:
. Die Selbstkonsistenzgl. liest sich:
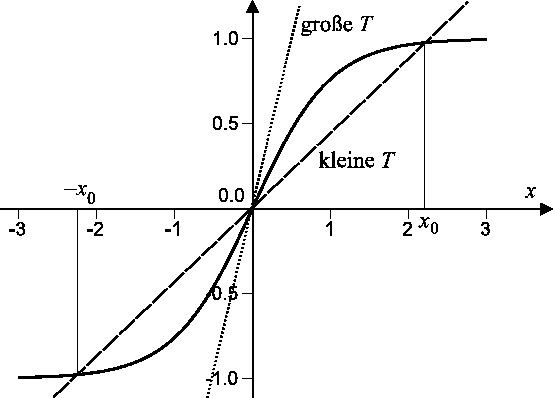
Bei hohen Temperaturen existiert nur eine Lösung, 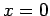 , d.h.
, d.h.
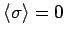 . Für niedrige Temperaturen: 3 Lösungen,
. Für niedrige Temperaturen: 3 Lösungen, 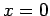 und
und 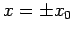 , d.h.
, d.h.
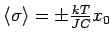 : Es entsteht eine spontane
Magnetisierung in Abwesenheit des Feldes, ein Zeichen des ferromagnetischen
Verhaltens. Der Übergang zwischen 2 Regime findet bei kritischer
Temperatur
: Es entsteht eine spontane
Magnetisierung in Abwesenheit des Feldes, ein Zeichen des ferromagnetischen
Verhaltens. Der Übergang zwischen 2 Regime findet bei kritischer
Temperatur 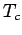 statt, wenn die Gerade
statt, wenn die Gerade
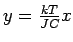 tangential zu
tangential zu 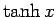 ist.
ist. 
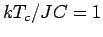
so dass



Nächste Seite: Verhalten in ferromagnetischen Bereich
Aufwärts: Die Molekularfeldnäherung (Mean field
Vorherige Seite: Hilfsaufgabe: Freie Spins im
Prof. Igor Sokolov
2004-07-01
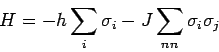
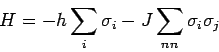
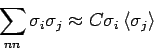
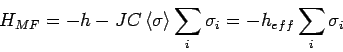
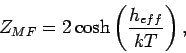
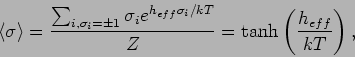
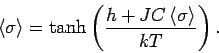
![]() , d.h.
, d.h.
![]() . Für niedrige Temperaturen: 3 Lösungen,
. Für niedrige Temperaturen: 3 Lösungen, ![]() und
und ![]() , d.h.
, d.h.
![]() : Es entsteht eine spontane
Magnetisierung in Abwesenheit des Feldes, ein Zeichen des ferromagnetischen
Verhaltens. Der Übergang zwischen 2 Regime findet bei kritischer
Temperatur
: Es entsteht eine spontane
Magnetisierung in Abwesenheit des Feldes, ein Zeichen des ferromagnetischen
Verhaltens. Der Übergang zwischen 2 Regime findet bei kritischer
Temperatur ![]() statt, wenn die Gerade
statt, wenn die Gerade
![]() tangential zu
tangential zu ![]() ist.
ist. ![]()
![]()