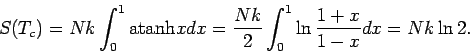![]() ,
, ![]() . Wir betrachten jetzt einige Spezialfälle.
. Wir betrachten jetzt einige Spezialfälle.
![]()
![]() . In diesem Fall
. In diesem Fall
![]() . Daher ist
. Daher ist
![]() und
und
![]() .
.
Erklärung:
![]() . Für
. Für
![]() sieht man, dass
sieht man, dass
![]() , so dass
, so dass
![]() und deswegen
und deswegen
![]() .
Diesen Wert kann jetzt in der rechte seite der Gl. eingestellt werden
(iteratives Lösen):
.
Diesen Wert kann jetzt in der rechte seite der Gl. eingestellt werden
(iteratives Lösen):
![]() und somit
und somit
![]() .
.
![]()
![]() . In diesem Fall
. In diesem Fall
![]() und somit
und somit
![]() . Es gilt
. Es gilt
![]() so dass
so dass
![]() .
Die nichttriviale Lösung der Gleichung ist:
.
Die nichttriviale Lösung der Gleichung ist:
![\begin{displaymath}
\left \langle \sigma \right \rangle = \left[ 3
\underbrace{...
...
\right]^{1/2 \displaystyle \leftarrow \mbox{krit. Exponente}}
\end{displaymath}](img820.png)
Innere Energie des Systems in MFA (![]() ).
).
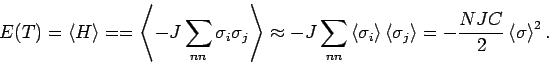
Spezifische Wärme (eigentlich, Spinanteil an der gesamten spezifischen
Wärme):
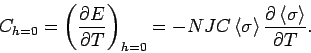
![]() Für
Für ![]() :
: ![]() und
und ![]() .
.
![]() Für
Für
![]() :
:
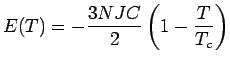 und
und
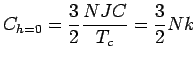
Die spezifische Wärme erfährt einen endlichen Sprung bei ![]()
![]() Für
Für
![]() :
:
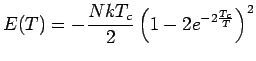 und
und
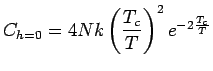 .
.
Die Entropie des Systems oberhalb ![]() bleibt konstant, da
bleibt konstant, da ![]() . Die
Entropie bei
. Die
Entropie bei ![]() ist:
ist:
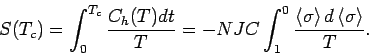
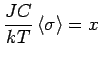 , anhand der MFA-Gleichung
, anhand der MFA-Gleichung