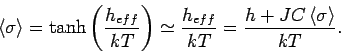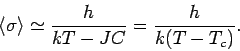Nächste Seite: Höhere Mean-Field-Näherungen
Aufwärts: Die Molekularfeldnäherung (Mean field
Vorherige Seite: Verhalten in ferromagnetischen Bereich
Betrachten wir die Situation beim Anlegen eines Felds 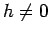 .
Selbstkonsistenzbedingung:
.
Selbstkonsistenzbedingung:
Auflösen nach
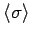 ergibt
ergibt
Daraus folgt für die Suszeptibilität (mit
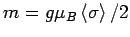 )
)
(das Curie-Weiß-Gesetz). Dieses Verhalten ist i.d.R. experimentell gut
bestätigt, allerdings liegt die so bestimmte 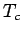 etwas oberhalb der
tatsächlicher Übergangstemperatur, z.B. für Ni ist
etwas oberhalb der
tatsächlicher Übergangstemperatur, z.B. für Ni ist 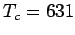 K, aus dem
Curie-Weiß-Gesetz bekommt man
K, aus dem
Curie-Weiß-Gesetz bekommt man 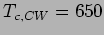 K.
K.
Prof. Igor Sokolov
2004-07-01