Idee: Die mean-field-artige Näherungen können beliebig verfeinert werden, in dem man nicht ein Spin in einem effektiven Feld, sondern eine Gruppe (Cluster) der Spins betrachtet. Die einfachste Näherung solcher Art ist die BETHE-Näherung.
Man betrachte eine Gruppe von Spins. Den zentrale Spin betrachtet man exakt,
die Wechselwirkungen seiner Nachbarn mit der Umgebung werden durch das
effektiven Feld ![]() beschrieben:
beschrieben:
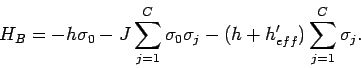
![\begin{displaymath}
Z=\sum_{\sigma_0 = \pm 1} \sum_{\sigma_j = \pm 1}
\exp \left...
...{C} \sigma_j
+ \gamma \sum_{j=1}^{C} \sigma_0 \sigma_j \right]
\end{displaymath}](img851.png)
![\begin{displaymath}
Z_\pm = \sum_{\sigma_j = \pm 1}
\exp \left[ \pm \alpha + (\a...
...alpha} \left[ 2 \cosh (\alpha + \alpha' \pm \gamma) \right]^C.
\end{displaymath}](img857.png)
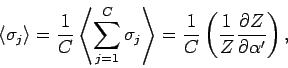
Spontane Magnetisierung (![]() ).
In diesem Fall ist
).
In diesem Fall ist ![]() . Das Logarithmieren der beiden seiten der
Gl.(22) ergibt:
. Das Logarithmieren der beiden seiten der
Gl.(22) ergibt:
![\begin{displaymath}
\alpha'=\frac{C-1}{2} \ln \left[\frac{\cosh(\alpha'+\gamma)}{\cosh(\alpha'-\gamma)}\right].
\end{displaymath}](img864.png)
![\begin{displaymath}
\alpha'=(C-1) \tanh \gamma \left[ \alpha' - \frac{\alpha'^3}{3} \mbox{sech}^2
\gamma + ... \right].
\end{displaymath}](img867.png)
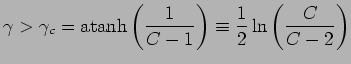 .
Auf Temperatur bezogen bedeutet das
.
Auf Temperatur bezogen bedeutet das
![\begin{displaymath}
T_c=\frac{2J}{k \ln[C/(C-2)]}.
\end{displaymath}](img870.png)
![]() Die Bethe-Näherung reproduziert die exakte Aussage über die
Abwesenheit des Phasenübergangs in einem eindimensionalen Ising-Modell
(für
Die Bethe-Näherung reproduziert die exakte Aussage über die
Abwesenheit des Phasenübergangs in einem eindimensionalen Ising-Modell
(für ![]() hat man
hat man ![]() ).
).
![]() Für große
Für große ![]() ist
ist
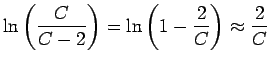 : Im Falle
grosser Zahlen der Nachbarn stimmen die einfache Molekularfeldnäherung und
die Bethe-Näherung überein. Die MF-Näherungen sind gut für
die höheren Dimensionen.
: Im Falle
grosser Zahlen der Nachbarn stimmen die einfache Molekularfeldnäherung und
die Bethe-Näherung überein. Die MF-Näherungen sind gut für
die höheren Dimensionen.