


Nächste Seite: Die Korrelationslänge
Aufwärts: Ising-Modell und verwandte Gittermodelle.
Vorherige Seite: Höhere Mean-Field-Näherungen
In 1D gibt es eine einfache, exakte Lösung, die durch die Transfermatrizen-
Methode geliefert wird (KRAMES und WANNIER, 1941).
Die Methode ist universal anwendbar für 1D Systeme; wir erläutern diese am
Beispiel des Ising-Modells.
Wir berechnen die Zustandssumme eines Ising-Systems auf einem Ring
(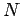 Gitterplatze), d.h. für periodische Randbedingungen. In thermodynamischen
Limes
Gitterplatze), d.h. für periodische Randbedingungen. In thermodynamischen
Limes
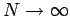 sollen sie keine Rolle spielen.
sollen sie keine Rolle spielen.
mit
Die
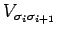 können als Elemente einer Matrix
können als Elemente einer Matrix
angesehen werden. Das Gesamtzustandssumme bekommt dann die folgende
Darstellung:
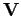 ist symmetrisch und kann diagonalisiert werden. In der
Diagonaldarstellung ist
ist symmetrisch und kann diagonalisiert werden. In der
Diagonaldarstellung ist
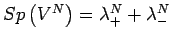 , wobei
, wobei 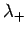 und
und 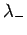 die Eigenwerte von
die Eigenwerte von 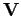 sind.
Für
sind.
Für
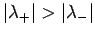 hat man im Grenzfall
hat man im Grenzfall
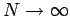
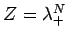 .
Die Eigenwerte der Matrize
.
Die Eigenwerte der Matrize 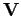 sind:
sind:
Daher, in thermodynamischen Grenzfall 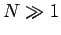
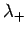 und somit
und somit 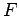 hat keine Pole, Nulstellen od. andere
Singularitäten für
hat keine Pole, Nulstellen od. andere
Singularitäten für 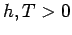
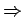 es gibt keinen Phasenübergang
bei
es gibt keinen Phasenübergang
bei 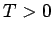 .
In Abwesenheit eines Feldes ist
.
In Abwesenheit eines Feldes ist
und
und
(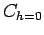 verschwindet für
verschwindet für 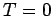 , wächst monoton an bei kleinem
, wächst monoton an bei kleinem
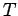 , hat einen Maximum
, hat einen Maximum 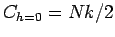 bei
bei 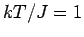 , und fällt dann
monoton ab).
Die Magnetisierung ist
, und fällt dann
monoton ab).
Die Magnetisierung ist
 Bei höheren Felder
Bei höheren Felder 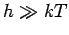 saturiert die
Magnetisierung.
saturiert die
Magnetisierung.
 Bei niedrigen Felder: Lineare Näherung
Bei niedrigen Felder: Lineare Näherung
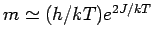 .
Die Suszeptibilität
.
Die Suszeptibilität
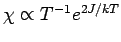 .
Für
.
Für
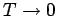 divergiert die Suszeptibilität: Es gibt einen
''Phasenübergang'' bei
divergiert die Suszeptibilität: Es gibt einen
''Phasenübergang'' bei 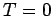 .
.
Unterabschnitte



Nächste Seite: Die Korrelationslänge
Aufwärts: Ising-Modell und verwandte Gittermodelle.
Vorherige Seite: Höhere Mean-Field-Näherungen
Prof. Igor Sokolov
2004-07-01
![]() Gitterplatze), d.h. für periodische Randbedingungen. In thermodynamischen
Limes
Gitterplatze), d.h. für periodische Randbedingungen. In thermodynamischen
Limes
![]() sollen sie keine Rolle spielen.
sollen sie keine Rolle spielen.
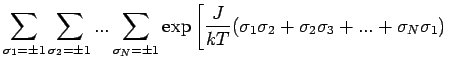
![$\displaystyle \left. + \frac{h}{kT}(\sigma_1 + \sigma_2 +...+ \sigma_N) \right]$](img877.png)
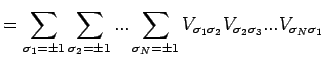
![\begin{displaymath}
V_{\sigma_i \sigma_{i+1}}=\exp \left[ \frac{J}{kT}\sigma_i \sigma_{i+1}
+\frac{h}{2kT} (\sigma_i + \sigma_{i+1}) \right].
\end{displaymath}](img879.png)
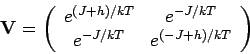
![\begin{displaymath}
F(N,T,h=0)= -kTN \ln \left[2 \cosh \left( \frac{J}{kT} \right) \right]
\end{displaymath}](img894.png)
![\begin{displaymath}
E(N,T,h=0)=-T^2 \left[ \frac{\partial}{\partial T} \left( \f...
...}
\right) \right]_{N,h}= -NJ \tanh \left( \frac{J}{kT}\right).
\end{displaymath}](img895.png)
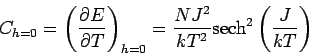
![\begin{displaymath}
m= - \left( \frac{\partial F}{\partial h} \right)_{T} =
\frac{\sinh (h/kT)}{[e^{4J/kT}+\sinh^2(h/kT)]^{1/2}}
\end{displaymath}](img900.png)
![]() Bei höheren Felder
Bei höheren Felder ![]() saturiert die
Magnetisierung.
saturiert die
Magnetisierung.
![]() Bei niedrigen Felder: Lineare Näherung
Bei niedrigen Felder: Lineare Näherung
![]() .
Die Suszeptibilität
.
Die Suszeptibilität
![]() .
Für
.
Für
![]() divergiert die Suszeptibilität: Es gibt einen
''Phasenübergang'' bei
divergiert die Suszeptibilität: Es gibt einen
''Phasenübergang'' bei ![]() .
.