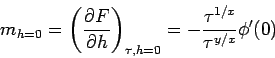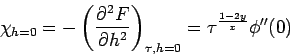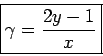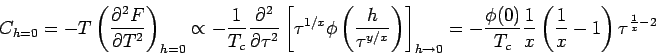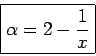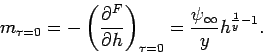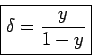Nächste Seite: Die Kadanoff-Konstruktion
Aufwärts: Moderne Theorie der Phasenübergänge
Vorherige Seite: Universalitätshypothese
Die Identitäten können durch die Annahme erklärt werden, dass in der Nähe von 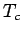
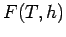 eine verallgemeinerte homogene Funktion der Parameter
eine verallgemeinerte homogene Funktion der Parameter 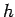 und
und 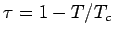 ist (hier ist
ist (hier ist
 ), d.h.
), d.h.
(z.B. für das 2d Ising Modell nahe am Übergang 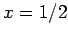 und
und 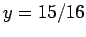 ).
Nehmen wir
).
Nehmen wir
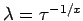 . So erhalten wir
. So erhalten wir
Daher:
Anderseits,
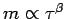

Weiterhin,
Anderseits,
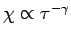

Für die spezifische Wärme hat man
Anderseits,
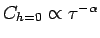

Für die Berechnung von 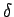 braucht man eine Umschreibung
braucht man eine Umschreibung
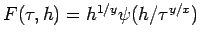 mit
mit
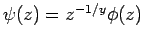 . Es wird angenommen, dass
. Es wird angenommen, dass
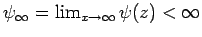 .
Dann ist
.
Dann ist
Daher
Kombinieren:
Das sind unsere (Un)Gleichungen (1) - (3).
Die Identitäten vom Typ (4) - (7) brauchen die FDT; wir werden sie auf einem anderen Wege bekommen.



Nächste Seite: Die Kadanoff-Konstruktion
Aufwärts: Moderne Theorie der Phasenübergänge
Vorherige Seite: Universalitätshypothese
Prof. Igor Sokolov
2004-07-01