Analogien zur klassische Mechanik

Nächste Seite: Die Wigner'sche Verteilungsfunktion. Aufwärts: Die Dichtematrix Vorherige Seite: Die Dichtematrix

Analogien zur klassische Mechanik

Analogie zur klassischen Liouville-Gleichung und das Korrespondenzprinzip:

Klassisch: $\rho$ - Wahrscheinlichkeitsdichte im Phasenraum. Normierung:

$\begin{displaymath} 1=\frac{1}{h^{3N}N!}\int ...\int d^{3N}qd^{3N}p\rho (\mathbf{q},\mathbf{p}). \end{displaymath}$

Für jede Funktion

$\begin{displaymath} \left\langle F\right\rangle =\frac{1}{h^{3N}N!}\int ...\int ... ...qd^{3N}p\rho (\mathbf{q},\mathbf{p})F(\mathbf{q},\mathbf{p}). \end{displaymath}$

Quantenmechnisch: $\rho$ - Dichtematrix. Normierung:

$\begin{displaymath} 1=\mbox{Sp}\rho \end{displaymath}$

Für jeden Operator

$\begin{displaymath} \left\langle F\right\rangle =\mbox{Sp}\left( \rho F\right) \end{displaymath}$

Die Bewegungsgleichungen:

Klassisch Quantenmechanisch

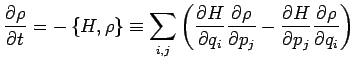$\displaystyle \frac{\partial \rho }{\partial t}=-\left\{ H,\rho \right\} \equiv... ...\frac{\partial H}{\partial p_{j}}\frac{\partial \rho } {\partial q_{i}}\right)$ $\displaystyle \frac{\partial \rho }{\partial t}= -\frac{i}{\hbar}\left[H,\rho \right]$

Für Gleichgewicht gilt $\left\{ H,\rho \right\} =0$ bzw. $\left[ H,\rho \right] =0$ .

Wichtiger Unterschied: die Verteilundsfunktion ist eine Funktion der Koordinaten und Impulse der Teilchen. Die Dichtematrix hängt nur von Koordinaten ab. Ist die Dichtematrix keine völlige quantenmechanische Analogie zur Verteilungsfunktion?

Prof. Igor Sokolov 2004-07-01

Klassisch	Quantenmechanisch
$\displaystyle \frac{\partial \rho }{\partial t}=-\left\{ H,\rho \right\} \equiv... ...\frac{\partial H}{\partial p_{j}}\frac{\partial \rho } {\partial q_{i}}\right)$	$\displaystyle \frac{\partial \rho }{\partial t}= -\frac{i}{\hbar}\left[H,\rho \right]$