Nächste Seite: Dichtematrix in Wigner-Darstellung:
Aufwärts: Die Dichtematrix
Vorherige Seite: Analogien zur klassische Mechanik
Einfachheitshalber, benutze ich hier die eindimensionale Notation.
Wigner-Repräsentation für eine mechanische Observable 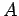 (Operator
(Operator 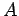 ):
):
Notation: Hier ist
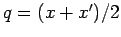 ,
,
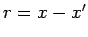 und
und
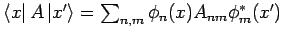 . Umschreiben:
. Umschreiben: 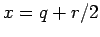 ,
,
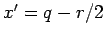 :
:
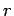 ist die Koordinate, und
ist die Koordinate, und 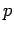 ist mít dem Impuls verbunden.
ist mít dem Impuls verbunden.
Betrachten wir die 2 Spezialfälle:

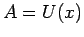 ist eine Funktion nur von der Koordinate. Dann folgt
ist eine Funktion nur von der Koordinate. Dann folgt
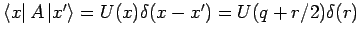

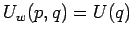 .
.

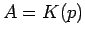 ist nur eine Funktion vom Impuls. Dann gilt
ist nur eine Funktion vom Impuls. Dann gilt
und
Um das zu sehen, nehmen wir an, dass
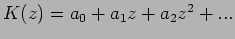 .
Dann ist das Glied 1. Ordnung
.
Dann ist das Glied 1. Ordnung
(partielle Integration). Die höhere Potenzen: analog, durch wiederholte
partielle Integration.
Prof. Igor Sokolov
2004-07-01
![]() (Operator
(Operator ![]() ):
):
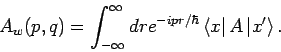
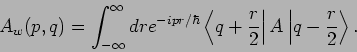
![]()
![]() ist eine Funktion nur von der Koordinate. Dann folgt
ist eine Funktion nur von der Koordinate. Dann folgt
![]()
![]()
![]() .
.
![]()
![]() ist nur eine Funktion vom Impuls. Dann gilt
ist nur eine Funktion vom Impuls. Dann gilt
![$\displaystyle K_{w}(p,q)=\int_{-\infty }^{\infty}dr
e^{-ipr/\hbar }K\left[ -i\h...
...\atop \mbox{auf nichts}}
+\frac{\partial }{\partial r}\right) \right] \delta(r)$](img1177.png)
![$\displaystyle =\int_{-\infty }^{\infty }dre^{-ipr/\hbar }K\left[ -i\hbar \frac{\partial}{\partial r}
\right] \delta (r)=K(p).$](img1178.png)