


Nächste Seite: Vibration
Aufwärts: Das ideale zweiatomige Gas:
Vorherige Seite: Das ideale zweiatomige Gas:
a) AB-Moleküle (unterschiedliche Atome) vom Typ
 mit
Atommassen
mit
Atommassen 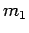 und
und 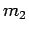 und dem Abstand zwischen den Atomen
und dem Abstand zwischen den Atomen 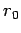 . Trägheitsmoment
. Trägheitsmoment
![$I=\left[ m_{1}m_{2}/(m_{1}+m_{2})\right] r_{0}^{2}$](img153.png) ,
,
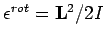 ,
, 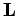 - Drehimpuls. Aus der
Quantenmechanik folgt dass
- Drehimpuls. Aus der
Quantenmechanik folgt dass 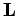 und z.B.
und z.B. 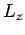 quantisiert sind,
quantisiert sind,
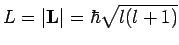 (mit
(mit 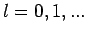 ) und
) und 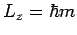 (mit
(mit 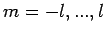 ). Dasaus folgt:
). Dasaus folgt:
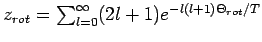 mit
mit
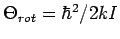 .
.
Die typische
Skalen für 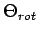 : für HD
: für HD
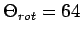 K, für NO
K, für NO
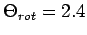 K.
K.
Folgerungen:
Für
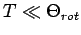 nur das term mit
nur das term mit 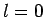 ist wichtig
ist wichtig 
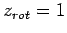 und die Rotation trägt nicht zur freien Energie bei
(''Einfrieren'' des Rotationsfreiheitsgrades).
und die Rotation trägt nicht zur freien Energie bei
(''Einfrieren'' des Rotationsfreiheitsgrades).
Sei nun
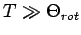 . Wechsel von Summation zur Integration:
. Wechsel von Summation zur Integration:
(Variablenwechsel
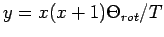 ). Damit ist
). Damit ist
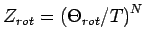 , so dass
, so dass
und
(Gleichverteilungssatz!).
b) Für Moleküle aus 2 gleichen Atomen, z.B. H , D
, D , O
, O u.s.w. treten aufgrund der Ununterscheidbarkeit der Atomkerne weitere
Quantenmechanische Effekte bei tiefen Temperaturen auf. Besonders wichtig bei H
u.s.w. treten aufgrund der Ununterscheidbarkeit der Atomkerne weitere
Quantenmechanische Effekte bei tiefen Temperaturen auf. Besonders wichtig bei H (Dennison & Hund, 1927): Para- und Orthowasserstoff.
(Dennison & Hund, 1927): Para- und Orthowasserstoff.
Der Hauptanteil der Rotationsenergie stammt von den Kernen. Es gibt 2 mö
gliche Einstellungen des Gesamtspins der Kerne:
Da die Gesamtwellenfunktion antisymmetrisch in Kernkoordinaten sein muss, sind die Spinanteil
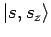 und Ortsanteil
nicht unabhängig.
und Ortsanteil
nicht unabhängig.
Singulet: Spinanteil
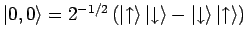 antisymmetrisch
antisymmetrisch  Ortsanteil symmetrisch, d.h.
Ortsanteil symmetrisch, d.h. 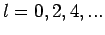
Triplet: 3 symmetrische Spinzustände
Ortsanteil antisymmetrisch, d.h. 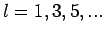 (Sieh Nolting, Aufgabe #
2.3.11).
(Sieh Nolting, Aufgabe #
2.3.11).

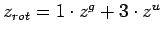 (die Summe der Singulett-
und Tripletbeiträge;
(die Summe der Singulett-
und Tripletbeiträge; 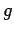 :
: 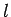 - gerade,
- gerade,
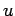 :
: 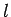 - ungerade) mit
- ungerade) mit
Insgesamt ergibt sich:
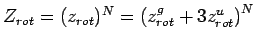 . Nun ist
. Nun ist
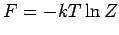 ;
;
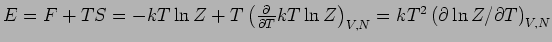 (Bemerkung: Hier erhalten wir
(Bemerkung: Hier erhalten wir 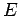 nicht als die Funktion ihrer natü
rlichen Variablen
nicht als die Funktion ihrer natü
rlichen Variablen 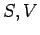 und
und 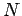 , sondern als Funktion von
, sondern als Funktion von 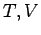 und
und 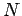 ) und
) und
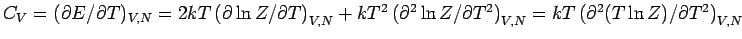 Exterimentell konnte diese Beziehung zunächst nicht nachgewiesen werden.
Grund dafür: Bei Änderung der Temperatur ist das Erreichen des
Gleichgewichtzustandes der Kernspins sehr langsam (Relaxationszeit: mehrere
Tage). Daher wurde experimentell nicht die Gleichgewichtseigenschaften der
Wasserstoff gemessen, sondern die Eigenschaften einer metastabilen Mischung
aus Ortho- und Parawasserstoff in seiner Hochtemperaturzusammensetzung (1
Teil Para- zu 3 Teile Orthowasserstoff):
Exterimentell konnte diese Beziehung zunächst nicht nachgewiesen werden.
Grund dafür: Bei Änderung der Temperatur ist das Erreichen des
Gleichgewichtzustandes der Kernspins sehr langsam (Relaxationszeit: mehrere
Tage). Daher wurde experimentell nicht die Gleichgewichtseigenschaften der
Wasserstoff gemessen, sondern die Eigenschaften einer metastabilen Mischung
aus Ortho- und Parawasserstoff in seiner Hochtemperaturzusammensetzung (1
Teil Para- zu 3 Teile Orthowasserstoff):
so dass
Die experimentelle Lösung wurde von Bonhoeffer und Harteck gefunden
(1929): Aktivkohle katalysiert die ortho-para-Übergänge.



Nächste Seite: Vibration
Aufwärts: Das ideale zweiatomige Gas:
Vorherige Seite: Das ideale zweiatomige Gas:
Prof. Igor Sokolov
2004-07-01
![]() mit
Atommassen
mit
Atommassen ![]() und
und ![]() und dem Abstand zwischen den Atomen
und dem Abstand zwischen den Atomen ![]() . Trägheitsmoment
. Trägheitsmoment
![]() ,
,
![]() ,
, ![]() - Drehimpuls. Aus der
Quantenmechanik folgt dass
- Drehimpuls. Aus der
Quantenmechanik folgt dass ![]() und z.B.
und z.B. ![]() quantisiert sind,
quantisiert sind,
![]() (mit
(mit ![]() ) und
) und ![]() (mit
(mit ![]() ). Dasaus folgt:
). Dasaus folgt:
![]() mit
mit
![]() .
.
![]() : für HD
: für HD
![]() K, für NO
K, für NO
![]() K.
K.
![]() nur das term mit
nur das term mit ![]() ist wichtig
ist wichtig ![]()
![]() und die Rotation trägt nicht zur freien Energie bei
(''Einfrieren'' des Rotationsfreiheitsgrades).
und die Rotation trägt nicht zur freien Energie bei
(''Einfrieren'' des Rotationsfreiheitsgrades).
![]() . Wechsel von Summation zur Integration:
. Wechsel von Summation zur Integration:
![]() und Ortsanteil
nicht unabhängig.
und Ortsanteil
nicht unabhängig.
![]() antisymmetrisch
antisymmetrisch ![]() Ortsanteil symmetrisch, d.h.
Ortsanteil symmetrisch, d.h. ![]()
![]()
![]() (die Summe der Singulett-
und Tripletbeiträge;
(die Summe der Singulett-
und Tripletbeiträge; ![]() :
: ![]() - gerade,
- gerade,
![]() :
: ![]() - ungerade) mit
- ungerade) mit
![\begin{displaymath}
C_{V}^{rot,metastabil}=NkT\left[ \frac{1}{4}\frac{\partial ...
...}}{%
\partial T^{2}}\left( T\ln z_{rot}^{u}\right) \right] .
\end{displaymath}](img194.png)