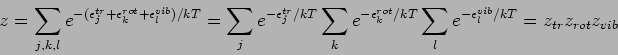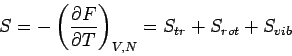Nächste Seite: Rotation.
Aufwärts: Die Kanonische Zustandssumme
Vorherige Seite: Der Gleichverteilungssatz der Energie
Hier: semiklassische Behandlung (Maxwell-Boltzmann Statistik), das System
aus 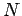 nicht-wechselwirkenden Molekülen
nicht-wechselwirkenden Molekülen
mit 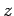 -Einteilchenzustandssumme,
-Einteilchenzustandssumme,
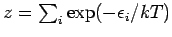 ,
, 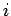 numeriert Energiezustände eines Moleküls.
Annahme: Enkopplung von Translations-, Rotations- und
Vibrationsfreiheitsgraden:
numeriert Energiezustände eines Moleküls.
Annahme: Enkopplung von Translations-, Rotations- und
Vibrationsfreiheitsgraden:

Die Gesamtzustandssumme lautet:
mit
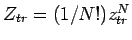 ,
,
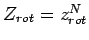 und
und
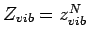 . Für die freie Energie erhält man:
. Für die freie Energie erhält man:
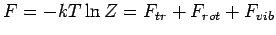 mit
mit
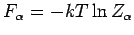 . Für die
Entropie erhält man
. Für die
Entropie erhält man
mit
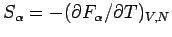 . Gleichermassen gilt
für die innere Energie:
. Gleichermassen gilt
für die innere Energie:
mit
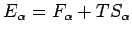 .
.
Wir betrachten jetzt getrennt die entsprechenden Komponenten der Bewegung.
Unterabschnitte
Prof. Igor Sokolov
2004-07-01