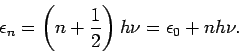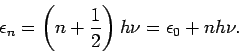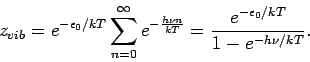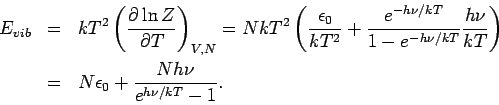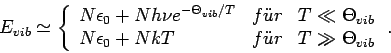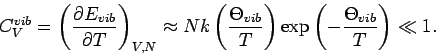Nächste Seite: Einstein-Modell des Kristalls
Aufwärts: Das ideale zweiatomige Gas:
Vorherige Seite: Rotation.
Annahme: Harmonische Schwingungen mit Eigenfrequenz 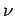 . Quantisierung der
Energie
. Quantisierung der
Energie
Die Einteilchenzustandssumme:
Die Vibrationsanteile an der Gesamtzustandssumme ist
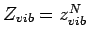 .
Daher lauten die Vibrationsbeiträge zu Thermodynamischen Eigenschaften
wie folgt:
.
Daher lauten die Vibrationsbeiträge zu Thermodynamischen Eigenschaften
wie folgt:
Mit
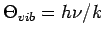 ist
ist
Für leichte zweiatomige Molekülen ist
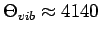 K für HCl und
K für HCl und
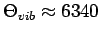 K für H
K für H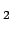 . Bei der
Zimmertemperatur ist daher
. Bei der
Zimmertemperatur ist daher
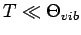 , so dass
, so dass
Die Vibrationsfreiheitsgrade solcher Moleküle sind
''eingefroren''. Für ein schwereres Molekül J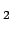 findet man
findet man
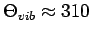 K, nahe der Zimmertemperatur. Für
K, nahe der Zimmertemperatur. Für
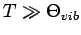 erhält man
erhält man
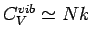 , im Einklang mit dem Gleichverteilungssatz.
, im Einklang mit dem Gleichverteilungssatz.
Prof. Igor Sokolov
2004-07-01