


Nächste Seite: Dichtematrizen für die drei
Aufwärts: Die Dichtematrix
Vorherige Seite: Dichtematrix in Wigner-Darstellung:
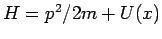 . Die Bewegungsgleichung für die Dichtematrix
. Die Bewegungsgleichung für die Dichtematrix
Variablenwechsel
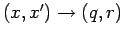 : Die rechte Seite geht
über in
: Die rechte Seite geht
über in
Benutzen wir jetzt die folgende Eigenschaften der Fourier-Transformation (
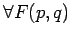 , so dass
, so dass
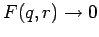 für
für
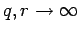 ):
):
(partielle Integration) und
(Taylorentwicklung von 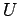 und die vorherige Gl.). Man bekommt
dann
und die vorherige Gl.). Man bekommt
dann
Das ist eine Gleichung, die die quantenmechanische Analogie zur
Liouville-Gleichung darstellt. In klassiscnem Limes
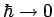 bekommt man
bekommt man
und die rechte Seite der Gleichung geht in den Liouville-Operator über.
Bemerkung: Für 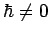 ist
ist 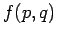 eine reelle
Funktion, allerdings keine Wahrscheinlichkeitsdichte, da sie sowohl positive
als auch negative Werte annehmen kann.
eine reelle
Funktion, allerdings keine Wahrscheinlichkeitsdichte, da sie sowohl positive
als auch negative Werte annehmen kann.
Prof. Igor Sokolov
2004-07-01
![]() . Die Bewegungsgleichung für die Dichtematrix
. Die Bewegungsgleichung für die Dichtematrix
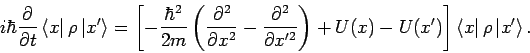
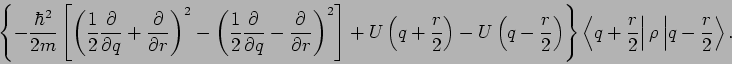
![]() , so dass
, so dass
![]() für
für
![]() ):
):
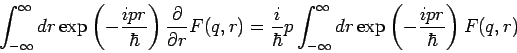
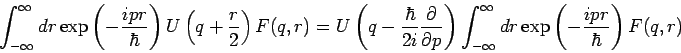
![\begin{displaymath}
\frac{\partial }{\partial t}f(p,q,t)=\left\{ -\frac{p}{m}\fr...
...ac{\partial }{%
\partial p}\right) \right] \right\} f(p,q,t).
\end{displaymath}](img1200.png)
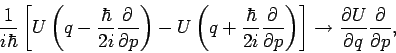
![]() ist
ist ![]() eine reelle
Funktion, allerdings keine Wahrscheinlichkeitsdichte, da sie sowohl positive
als auch negative Werte annehmen kann.
eine reelle
Funktion, allerdings keine Wahrscheinlichkeitsdichte, da sie sowohl positive
als auch negative Werte annehmen kann.