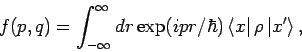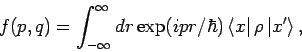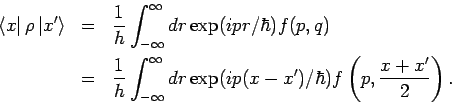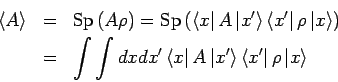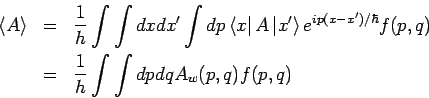Nächste Seite: Bewegungsgleichung für die Wignerfunktion.
Aufwärts: Die Dichtematrix
Vorherige Seite: Die Wigner'sche Verteilungsfunktion.
Wiegner'sche Verteilungsfunktion. Die Umkehrtransformation lautet:
Benutzen wir jetzt die Eigenschaft
Unter Benutzung des vorherigen Gleichung erhalen wir:
(Variablenwechsel
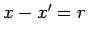 ,
,
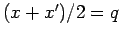 ). In
Wigner-Notation also
). In
Wigner-Notation also
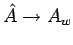 ,
,
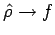 ,
,
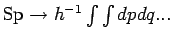 .
.
Prof. Igor Sokolov
2004-07-01