Nächste Seite: Großkanonische Gesamtheit
Aufwärts: Kanonische Gesamtheit
Vorherige Seite: Kanonische Gesamtheit
Wir betrachten hier nur das Beispiel der Teilchen in 1 Dimension.
mit
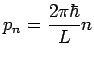 (flache Wellen als vollständige Basis für die Berechnung der
Dichtematrix). Das Hamilton-Operator
(flache Wellen als vollständige Basis für die Berechnung der
Dichtematrix). Das Hamilton-Operator
Jetzt können wir 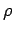 ausrechnen. Dafür brauchen wir den Ausdruck für
ausrechnen. Dafür brauchen wir den Ausdruck für
Für eine beliebige hinreichend differenzierbare Funktion 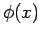 gilt:
gilt:
(Produktregel).
Nach 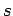 -maliger Anwendung dieses Verfahrens bekommen wir:
-maliger Anwendung dieses Verfahrens bekommen wir:
so dass
und das Operator 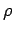 ist:
ist:
Daher lautet die Zustandssumme
Für
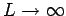 : Kontinuumübergang
: Kontinuumübergang
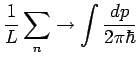 .
Klassischer Übergang als formaler Übergang
.
Klassischer Übergang als formaler Übergang
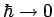 im
Integral:
im
Integral:
Wenn das System aus 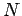 Teilchen besteht, kann über ihre Koordinaten
unabhängig integriert, und dann durch Anzahl der Permutationen dividiert
werden. Man bekommt den klassischen Ausdruck
Teilchen besteht, kann über ihre Koordinaten
unabhängig integriert, und dann durch Anzahl der Permutationen dividiert
werden. Man bekommt den klassischen Ausdruck



Nächste Seite: Großkanonische Gesamtheit
Aufwärts: Kanonische Gesamtheit
Vorherige Seite: Kanonische Gesamtheit
Prof. Igor Sokolov
2004-07-01
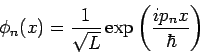
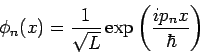
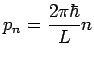 (flache Wellen als vollständige Basis für die Berechnung der
Dichtematrix). Das Hamilton-Operator
(flache Wellen als vollständige Basis für die Berechnung der
Dichtematrix). Das Hamilton-Operator
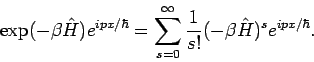
![\begin{displaymath}
\hat{H} e^{ipx/\hbar} \phi(x) = e^{ipx/\hbar}
\left[ \frac{...
... \frac{\hbar}{i}
\frac{d}{dx} \right)^2 +U(x) \right] \phi(x)
\end{displaymath}](img1257.png)
![\begin{displaymath}
\hat{H}^s e^{ipx/\hbar} \phi(x) = e^{ipx/\hbar}
\left[ \fra...
...rac{\hbar}{i}
\frac{d}{dx} \right)^2 +U(x) \right]^s \phi(x),
\end{displaymath}](img1258.png)
![\begin{displaymath}
\exp( -\beta \hat{H}) e^{ipx/\hbar} \phi(x) = e^{ipx/\hbar} ...
...ar}{i}
\frac{d}{dx} \right)^2 +U(x) \right] \right\} \phi(x),
\end{displaymath}](img1259.png)
![\begin{displaymath}
\rho(x,x') = \frac{1}{L} \sum_n e^{ip_n(x-x')/\hbar}
\exp \...
...frac{\hbar}{i}
\frac{d}{dx} \right)^2 +U(x) \right] \right\}.
\end{displaymath}](img1260.png)
![\begin{displaymath}
Z= \int_0^L \rho(x,x)dx = \frac{1}{L} \sum_n \int_0^L
\exp ...
...c{\hbar}{i}
\frac{d}{dx} \right)^2 +U(x) \right] \right\} dx.
\end{displaymath}](img1261.png)
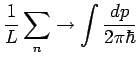 .
Klassischer Übergang als formaler Übergang
.
Klassischer Übergang als formaler Übergang