Destilliertes Wasser

Für Wasser wurde der komplexe Brechungsindex von verschiedenen Autoren gemessen. Der Imaginärteil k ergibt sich durch Absorptionsmessungen an keilförmigen Absorptionszellen [Downing, Williams, 75]. Der Realteil n wird hauptsächlich aus Reflexionsmessungen gewonnen. Für verschiedene Spektralbereiche müssen unterschiedliche Detektoren und Me\3aufbauten verwendet werden. Aufgrund der experimentellen Schwierigkeiten und der extrem geringen Eindringtiefe von Infrarotstrahlung in Wasser, ergeben sich signifikante Abweichungen zwischen den veröffentlichten Resultaten ([Irvine, Pollack, 68]), speziell für den Imaginärteil k. Die umfangreichste (und gleichzeitig vertrauenswürdigste) Sammlung für reines (destilliertes) Wasser findet sich bei [Downing, Williams, 75]. Sie deckt den kompletten Spektralbereich von 2 bis 1000m ab.

nlambda

  
Abbildung: Realteil des komplexen Brechungsindexes N (Daten aus [Downing, Williams, 75]).

klambda

  
Abbildung: Imaginärteil des komplexen Brechungsindexes N (Daten aus [Downing, Williams, 75]).

Für den Spektralbereich von 2 bis 100m sind diese Daten in den Abbildungen 2.15 und 2.16 dargestellt. Sie zeigen jeweils den Realteil n bzw. den Imaginärteil k des komplexen Brechungsindexes von reinem Wasser. Die grö\3te Variation für diese beiden Grö\3en liegt im Bereich von 2 bis 20m. Dort befinden sich Absorptionsbanden des Wassermoleküls. Innerhalb dieses Bereichs (von 3-5m) ist die AMBER Radiance 1 Kamera empfindlich und der verwendete CO-Laser emittiert Strahlung bei 10.6m. Daher sind alle Darstellungen der optischen Eigenschaften von Wasser im folgenden über einer logarithmischen Wellenlängenskala geplottet, um den Bereich für kleine Wellenlängen detaillierter aufzulösen.

Aus diesen Werten von n und k lassen sich nun die me\3baren optischen Eigenschaften von Wasser ableiten. Aus (2.69) ergibt sich der Absorptionskoeffizient und damit die Eindringtiefe ({2.70) für verschiedene Wellenlängen. Abbildung 2.17 zeigt diese für das Wellenlängenintervall von 2 bis 100m in doppelt-logarithmischer Darstellung.

betazeta

  
Abbildung: Absorptionskoeffizient und Eindringtiefe für Wasser (berechnet mit den Daten für aus [Downing, Williams, 75]).

Erkennbar ist, da\3 innerhalb des empfindlichen Spektralbereiches der AMBER Kamera die Eindringtiefe über zwei Grö\3enordnungen variiert! Daher kann keine gemittelte Eindringtiefe für den gesamten Bereich von 3-5m angegeben werden. Speziell bei gro\3en Temperaturgradienten innerhalb der oberen 100m der Wasseroberfläche mu\3 dies bei der Interpretation des Kamerabildes berücksichtigt werden (siehe Kapitel 2.4.3).

Eine weitere Grö\3e, die zur Abschätzung der Me\3fehler in Thermographiebildern der Meeresoberfläche wichtig wird, ist die mittlere Reflektivität der Wasseroberfläche (bei senkrechter Beobachtung) im Wellenlängenintervall der Kamera und bei der Laser-Wellenlänge. In Tabelle 2.1 sind die aus [Downing, Williams, 75] berechneten Mittelwerte für n und k zwischen 3-5m und die Werte für n und k bei der Wellenlänge des CO-Lasers (10.6m) zusammengestellt. Die Reflektivität und die Emissivität ergeben sich damit aus (2.71).

 
Tabelle:   Zusammenstellung von Brechungsindex, Reflektivität und Emissivität bei 3-5m (Mittelwerte) und 10.6m.

Erkennbar ist, da\3 bei 10.6m die Emissivität grö\3er als 0.99 ist. Für den CO-Laser verhält sich die Wasseroberfläche fast wie ein schwarzer Strahler. Bei senkrechter Einstrahlung wird die Laserleistung zu mehr als 99% absorbiert. Im Wellenlängenintervall der Kamera bei 3-5m ist die Reflektivität mehr als drei mal so gro\3. Für beliebige Wellenlängen ergibt sich mit den Daten für und aus (2.71) die spektrale Reflektivität

für sehr kleine Winkel () gegen das Einfallslot. Abbildung 2.18 zeigt den Verlauf der spektralen Reflektivität für Wellenlängen von 2 bis 100m.

rhosenkrecht

  
Abbildung: Reflektivität für Wasser (berechnet mit den Daten für und aus [Downing, Williams, 75]).

Der qualitative Verlauf ähnelt der Kurve für den Realteil des Brechungsindexes (Abb. 2.15). Die spektrale Reflektivität variiert jedoch über zwei Grö\3enordnungen, während nur Werte zwischen 1 und 2 annimmt. Die horizontale Linie zeigt den Mittelwert () der Reflektivität für das dargestellte Wellenlängenintervall. Daraus ist ersichtlich, da\3 sich in der Nähe der Laser-Wellenlänge ein lokales Minimum der Reflektivität befindet.

Für einen bestimmten Brechungsindex lä\3t sich aus den Fresnel'schen Gleichungen (2.73) und (2.74) die Winkelabhängigkeit der Reflektivität berechnen. Dies wurde für die beiden Realteile n des Brechungsindexes in Tabelle 2.1 durchgeführt. Die Abbildungen 2.19a und 2.19b zeigen die Komponenten und für Winkel von 0 bis 90. Zusätzlich ist in beiden Abbildungen noch das arithmetische Mittel (2.75) eingezeichnet, welches für unpolarisierte Strahlung die effektive Reflektivität darstellt.

rhowinkel

  
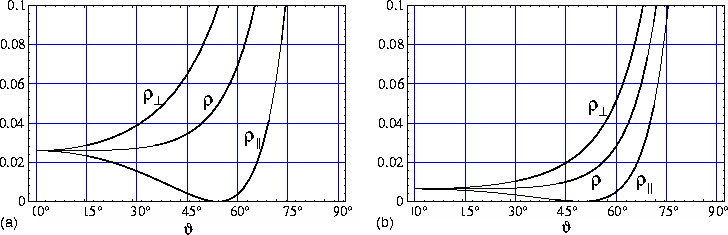
Abbildung: Winkelabhängigkeit der Reflektivität für unterschiedliche Polarisationsrichtungen der Strahlung. (a): Mittelwert für den Wellenlängenbereich 3-5m. (b): Wellenlänge des CO-Lasers (10.6m).

Erkennbar ist, da\3 die Reflektivität für Strahlung, die senkrecht zur Einfallsebene polarisiert ist, mit wachsendem Winkel zunimmt. Für eine Polarisationsrichtung parallel zur Einfallsebene nimmt die Reflektivität dagegen zunächst ab. Beim Brewster-Winkel () verschwindet sie völlig und steigt danach wieder stark an. Für beide Polarisationsrichtungen erreicht die Reflektivität den Wert 1 bei 90. Der Mittelwert aus beiden Polarisationsrichtungen bleibt zunächst konstant. Der Abfall der Komponente kompensiert den Anstieg der Komponente . Für Winkel oberhalb des Brewster-Winkels steigt auch steil an und damit der Mittelwert . Dies führt zu dem interessanten und wichtigen Ergebnis, da\3 die Reflektivität - und damit auch die Emissivität () - von Wasser für Winkel bis zum Brewster-Winkel nahezu konstant ist. Dieser beträgt für Wasser im Infraroten 55 (für ). Die Wasseroberfläche lä\3t sich somit innerhalb dieses Winkelbereiches in guter Näherung als Lambertscher Strahler annehmen und es gilt:

Abbildung 2.20 zeigt nochmals den Verlauf von und für unpolarisierte Strahlung über die volle Skala von 0 bis 1.

rhoundtheta

  
Abbildung: Winkelabhängigkeit der Reflektivität und der Emissivität für unpolarisierte Strahlung (Mittelwert für den Wellenlängenbereich 3-5m).

Für Winkel oberhalb des Brewserwinkels steigt die Reflektivität schnell gegen 1 an, d. h. für gro\3e Winkel verhält sich Wasser wie ein Spiegel. Bei Temperaturmessungen mu\3 daher darauf geachtet werden, da\3 der Strahlungsdetektor weitgehend senkrecht auf die Wasseroberfläche blickt.

Der unterschiedliche Verlauf von und lä\3t sich gezielt ausnutzen. Der verwendete CO-Laser emittiert Strahlung, die zu 98% linear, senkrecht zur Ausbreitungsrichtung polarisiert ist. Die Anordnung der Spiegel im optischen Aufbau der CFT-Maschine wurde so gewählt, da\3 die Laser-Strahlung parallel zur Einfallsebene polarisiert auf das Wasser auftrifft. Der Blickwinkel der Kamera und die Einstrahlrichtung des Lasers betragen 20 gegen die Senkrechte (). Wie aus Abbildung 2.19b ersichtlich ist, reduziert sich die Reflektivität für den Laser dadurch nochmals um 22% gegenüber unpolarisierter Strahlung. Die Reflektivität für unpolarisierte Strahlung, die die Kamera von der Wasseroberfläche empfängt, ändert sich dabei um weniger als 3% im Vergleich zu senkrechter Blickrichtung.