- ... Entartung).1
- Diese Entartung hängt mit der Existenz von einem zusätzlichen Operator zusammen,
der (zusammen mit
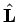 und
und 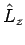 ) mit
) mit 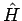 kommutiert.
Dieses ist der sog.LENZ-vektor (oder Laplace-Runge-Lenz Vektor)
kommutiert.
Dieses ist der sog.LENZ-vektor (oder Laplace-Runge-Lenz Vektor)
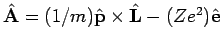 mit
mit 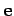 - Einheitsvektor in
- Einheitsvektor in 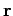 -Richtung. Dieser Operator entspricht
einem zusätzlichen klassischen Bewegungsintegral im Coulombfeld, siehe
C.E. Burkhardt, J.J. Leventhal, Am. J. Phys. 72, 1013 (2004)
-Richtung. Dieser Operator entspricht
einem zusätzlichen klassischen Bewegungsintegral im Coulombfeld, siehe
C.E. Burkhardt, J.J. Leventhal, Am. J. Phys. 72, 1013 (2004)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... betrachten2
- Die Ableitung einer Operatorfunktion nach einem Operator kann mathematisch
als Grenzwert
![$\frac{d}{d\hat{A}}f(\hat{A})=\lim_{\varepsilon \rightarrow
0}\left[ \frac{1}{\varepsilon }\left( f(\hat{A}+\varepsilon \hat{I})-f(%
\hat{A}\right) \right] $](img1815.png) definirt werden. Für eine so definierte
Ableitung gelten die üblichen Regel (Linearität, Kettenregel,
u.s.w; man beachte aber die Reihenfolge der Operatoren!
definirt werden. Für eine so definierte
Ableitung gelten die üblichen Regel (Linearität, Kettenregel,
u.s.w; man beachte aber die Reihenfolge der Operatoren!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Inverse3
- Wie wir es sehen werden, kann man oft trotzdem so verfahren, als ob dieser
Operator immer eine Inversen besitzt. Wenn man sicher gehen will, kann man
einen Trick benutzen, und dem noch nicht festgelegten
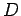 einen kleinen
imaginären Teil geben:
einen kleinen
imaginären Teil geben:
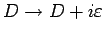 . Dieser garantiert
die Invertierbarkeit, da die Eigenwerte von
. Dieser garantiert
die Invertierbarkeit, da die Eigenwerte von 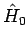 allesamt reell
sind. Am Ende soll man den Grenzwert bei
allesamt reell
sind. Am Ende soll man den Grenzwert bei
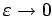 nehmen.
Falls dieser existiert, ist unsere Störungsreihe OK.
nehmen.
Falls dieser existiert, ist unsere Störungsreihe OK.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![$\frac{d}{d\hat{A}}f(\hat{A})=\lim_{\varepsilon \rightarrow
0}\left[ \frac{1}{\varepsilon }\left( f(\hat{A}+\varepsilon \hat{I})-f(%
\hat{A}\right) \right] $](img1815.png) definirt werden. Für eine so definierte
Ableitung gelten die üblichen Regel (Linearität, Kettenregel,
u.s.w; man beachte aber die Reihenfolge der Operatoren!
definirt werden. Für eine so definierte
Ableitung gelten die üblichen Regel (Linearität, Kettenregel,
u.s.w; man beachte aber die Reihenfolge der Operatoren!