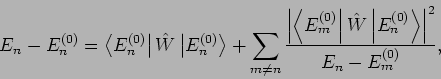Next: Vielteilchensysteme I
Up: Zeitunabhängige Störungstheorie
Previous: Rechenbeispiel 2: Abschätzung der
Contents
Das Problem der Störungstheorien lässt sich allgemeiner formulieren.
Wir gehen aus von den Eigenschaften
und benutzen die spezielle Normierungsvorschrift
(in 1. Ordnung ist das automatisch erfüllt; die WF höherer Ordnungen
müssen nachnormiert werden!). Aus solcher Normierung folgt
und
Daher ist die exakte Niveauverschiebung
Wir definieren den Projektionsoperator
und
Es gilt
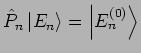 .
. 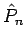 und
und 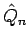 kommutieren mit
kommutieren mit 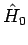 :
:
![$\left[ \hat{P}_{n},\hat{H}_{0}\right] =\left[ \hat{Q}_{n},%
\hat{H}_{0}\right] =0$](img2003.png) .
.
Schreiben wir die Eigenwertsgleichung wie folgt um:
(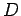 - eine reelle Zahl). Der Operator
- eine reelle Zahl). Der Operator
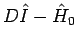 besitzt eine
Inverse3, falls
besitzt eine
Inverse3, falls 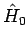 keinen Eigenwert besitzt, dass
keinen Eigenwert besitzt, dass 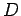 gleich ist. Daher:
gleich ist. Daher:
Benutzen wir jetzt die Projektionsoperatoren:
Die Gleichung lässt sich iterieren. Der Operator 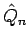 kommutiert mit
kommutiert mit
und ist idempotent,
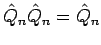 . Daher
. Daher
Die Niveauverschiebung ist dann
Da
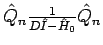 das Niveau
das Niveau 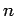 aus
der Summierung ausschliesst, ist es eigentlich möglich
aus
der Summierung ausschliesst, ist es eigentlich möglich 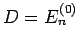 anzunehmen. Daher bis zum
anzunehmen. Daher bis zum 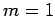
Formen wir das 2. Glied um durch explizite Ausschreibung von dem ersten 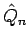
Schreiben wir den zweiten 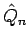 explizit aus:
explizit aus:
Der Operator
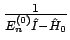 ist in der
Energiedarstellung des ungestörten Problem diagonal, so dass
ist in der
Energiedarstellung des ungestörten Problem diagonal, so dass
und die Summe über 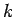 entfällt.
entfällt.
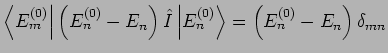 , und gibt keinen Beitrag
für
, und gibt keinen Beitrag
für 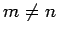 . Man erhällt also
. Man erhällt also
unsere gewohnte Gleichung für die Störungstheorie 2. Ordnung.
Die Wahl 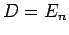 , noch unbekannter Energie, ergibt gleichermassen in 2.
Ordnung
, noch unbekannter Energie, ergibt gleichermassen in 2.
Ordnung
das Brillouin-Wigner'sches Resultat.




Next: Vielteilchensysteme I
Up: Zeitunabhängige Störungstheorie
Previous: Rechenbeispiel 2: Abschätzung der
Contents
Prof. Igor Sokolov
2005-02-14
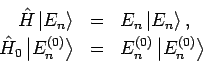
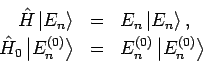
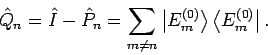
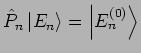 .
. ![$\left[ \hat{P}_{n},\hat{H}_{0}\right] =\left[ \hat{Q}_{n},%
\hat{H}_{0}\right] =0$](img2003.png) .
.
![\begin{eqnarray*}
\left\vert E_{n}\right\rangle &=&\hat{P}_{n}\left\vert E_{n}\r...
...n}\right) \hat{I}+\hat{W}\right] \left\vert
E_{n}\right\rangle .
\end{eqnarray*}](img2009.png)
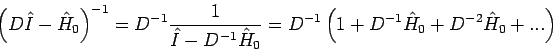
![\begin{displaymath}
\left\vert E_{n}\right\rangle =\left\vert E_{n}^{(0)}\right\...
...at{W}\right] \right\} ^{m}\left\vert
E_{n}^{(0)}\right\rangle
\end{displaymath}](img2012.png)
![\begin{displaymath}
E_{n}-E_{n}^{(0)}=\left\langle E_{n}^{(0)}\right\vert \hat{W...
...{W}\right] \right\} ^{m}\left\vert
E_{n}^{(0)}\right\rangle .
\end{displaymath}](img2013.png)
![\begin{displaymath}
E_{n}-E_{n}^{(0)}=\left\langle E_{n}^{(0)}\right\vert \hat{W...
... \hat{I}+\hat{W}\right] \left\vert E_{n}^{(0)}\right\rangle .
\end{displaymath}](img2017.png)
![\begin{eqnarray*}
&&\left\langle E_{n}^{(0)}\right\vert \hat{W}\hat{Q}_{n}\frac{...
...ht) \hat{I}+\hat{W}%
\right] \left\vert E_{n}^{(0)}\right\rangle
\end{eqnarray*}](img2019.png)
![\begin{eqnarray*}
&&\sum_{m\neq n}\sum_{k\neq n}\left\langle E_{n}^{(0)}\right\v...
...\right\vert \hat{W}\left\vert E_{n}^{(0)}\right\rangle
\right] .
\end{eqnarray*}](img2020.png)
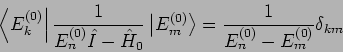
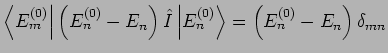 , und gibt keinen Beitrag
für
, und gibt keinen Beitrag
für 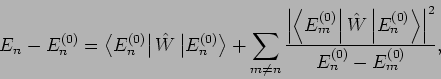
![]() , noch unbekannter Energie, ergibt gleichermassen in 2.
Ordnung
, noch unbekannter Energie, ergibt gleichermassen in 2.
Ordnung