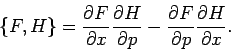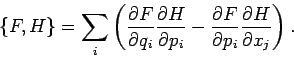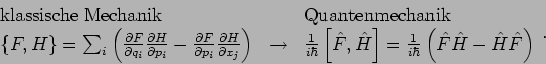Next: Evolution der Mittelwerte
Up: Heisenberg-Bild.
Previous: Bewegungsintegrale
Contents
Obwohl das Schrödinger-Bild zu der Schrödinger-Gleichung für die
Wellenfunkzion führt, die einfacher zu lösen ist, als die
Heisenberg-Gl. für die Operatoren, finden einige Eingeschaften der
Bewegung der Quantensysteme im Heisenbeg-Bild ihre einfachere Darstellung.
Betrachten wir ein Quantensystem, das ein klassisches Analog besitzt (kein
Spin!), und vergleichen wir die Eigenschaften der beiden Beschreibungen. Es
gilt:
und
Der Hamiltonian 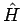 lässt sich schreiben als
lässt sich schreiben als
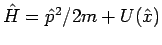 (in dem Fall des Magnetfeldes gibt es noch
Mischglieder). Wir betrachten nun
(in dem Fall des Magnetfeldes gibt es noch
Mischglieder). Wir betrachten nun 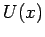 als eine analytische Funktion von
als eine analytische Funktion von 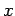 (Taylor-Entwicklung) und benutzen die Eigenschaften
(Taylor-Entwicklung) und benutzen die Eigenschaften
und
(wobei wir die Differenzierung nach einem Operator rein formal betrachten2) so bekommen wir
und
was als vollständiges quantenmechanisches Analogon zu den klassischen
Hamilton-Gl'en
betrachtet werden kann.
Die allgemeine Bewegungsgleichung für eine Messbaren 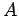 in der
Quantenmechanik, Gl.(47), hat ihre klassische Entsprechung in der
Bewegungsgleichung
in der
Quantenmechanik, Gl.(47), hat ihre klassische Entsprechung in der
Bewegungsgleichung
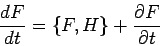 |
(48) |
(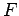 --eine klassisch Messbare, eine Fkt. von
--eine klassisch Messbare, eine Fkt. von 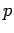 und
und 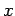 ), wobei
), wobei
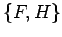 eine Poissonklammer ist,
eine Poissonklammer ist,
Das gleiche gilt in höheren Dimensionen, mit
Die klassische Gl.(48) ist identisch in Form mit der
quantenmechanischen Gl.(47), wenn man den Kommutator als
quantenmechanisches Pendant zur Poissonklammer betrachtet:




Next: Evolution der Mittelwerte
Up: Heisenberg-Bild.
Previous: Bewegungsintegrale
Contents
Prof. Igor Sokolov
2005-02-14
![\begin{displaymath}
\left[ \hat{x},\hat{p}^{n}\right] =ni\hbar \hat{p}^{n-1}\equiv i\hbar \frac{d}{d\hat{p}}\hat{p}^{n}
\end{displaymath}](img1813.png)
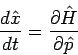
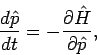
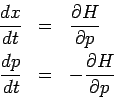
![]() in der
Quantenmechanik, Gl.(47), hat ihre klassische Entsprechung in der
Bewegungsgleichung
in der
Quantenmechanik, Gl.(47), hat ihre klassische Entsprechung in der
Bewegungsgleichung