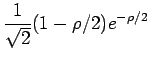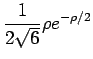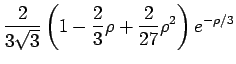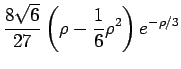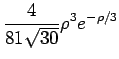Next: Mathematischer Einschub: Die zugeordneten
Up: Allgemeine Eigenschaften der Bewegung
Previous: Allgemeine Eigenschaften der Bewegung
Contents
Für das Wasserstoffatom und (mehrfach) ionisierte Atome He , Li
, Li u.s.w. hat die radiale SGl. die Gestalt
u.s.w. hat die radiale SGl. die Gestalt
(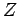 - Kernladung. Der Kern wird als festgehalten vorausgesetzt, sonst
- Kernladung. Der Kern wird als festgehalten vorausgesetzt, sonst
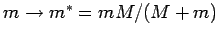 , mit
, mit 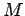 -Masse des Atomkerns).
-Masse des Atomkerns).
Es ist bequemer, charakteristische Größen einzuführen und die Gl.
in einer dimensionslosen Form zu schreiben:
- atomere Längeneinheit: der Bohr'sche Radius
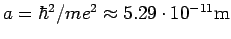
- atomere Energieeinheit
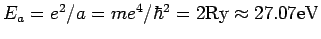 .
.
Unter Verwendung der dimensionslosen Größen 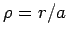 und
und
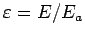 erhält man
erhält man
![\begin{displaymath}
\left[ \frac{d^{2}}{d\rho ^{2}}+2\varepsilon +\frac{2Z}{\rho }-\frac{l(l+1)}{%
\rho ^{2}}\right] R(\rho )=0.
\end{displaymath}](img1157.png) |
(28) |
Die Fkt. 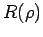 muß für
muß für
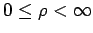 definiert sein und
genügt der natürlichen Randbedingung
definiert sein und
genügt der natürlichen Randbedingung
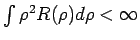 . Da die potentielle Energie im Unendlichen verschwindet,
gehören die gebundenen Zustände zu negativen Werten von
. Da die potentielle Energie im Unendlichen verschwindet,
gehören die gebundenen Zustände zu negativen Werten von 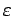 . Daher ist es zweckmäßig eine positive Größe einzuführen
. Daher ist es zweckmäßig eine positive Größe einzuführen
Die Ls'gen mit endlicher Energie existieren nur, wenn 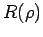 für
für
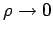 hinreichend schnell veschwindet, also
hinreichend schnell veschwindet, also 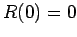 . Die
asymptotische Lsg. für
. Die
asymptotische Lsg. für
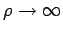
Aus der Randbedingung folgt 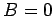 .
.
Die Lösung wird in Form
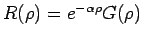 geschrieben, wobei
geschrieben, wobei 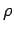 in Form einer Potenzreihe gesucht wird. Da die
Reihe nicht mit dem Glied
in Form einer Potenzreihe gesucht wird. Da die
Reihe nicht mit dem Glied 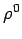 anfängt, schreiben wir
anfängt, schreiben wir
Setzen wir die Reihe in der Gl.(28) ein und betrachten nur die
kleinsten Potenzen von 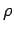 , so gilt es (aus der 2. Abl. und der
, so gilt es (aus der 2. Abl. und der 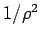 -Glieder)
-Glieder)
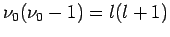 , d.h.
, d.h.
Die Lsg. 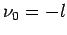 ist durch die Randbedingung
ist durch die Randbedingung 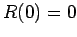 verboten. Die
Lsg. ist also
verboten. Die
Lsg. ist also
Diese Ausdruck wird in die radiale Gl. eingesetzt. Aus dem
Koeffizientenvergleich erhalten wir dann
Bricht die Reihe ab, so erhalten wir ein Polynom in 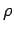 (proportional
zu dem sog. zugeordneten LAGUERRE'schen Polynom).
Sonst bekommt man für
(proportional
zu dem sog. zugeordneten LAGUERRE'schen Polynom).
Sonst bekommt man für 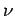 groß
groß
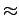 die Entwicklungskoeffizienten der Funktion
die Entwicklungskoeffizienten der Funktion
Die Funktion wächst schneller als
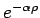 abklingt, die
ganze WF wird daher nicht normierbar.
abklingt, die
ganze WF wird daher nicht normierbar.
Die Reihe bricht ab, wenn bei irgendeinem 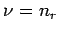
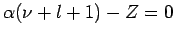 ist. Daher ist
ist. Daher ist
eine ganze Zahl. Die Kombination 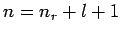 ist die Hauptquantenzahl,
so dass die Energie der stationären Zustände
ist die Hauptquantenzahl,
so dass die Energie der stationären Zustände
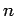 nimmt alle positiven ganzen Zahlen von 1 ab an.
nimmt alle positiven ganzen Zahlen von 1 ab an.
Die Energie hängt nur von 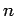 ab; die Quantenzahl
ab; die Quantenzahl 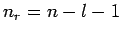 gibt die Anzahl der Knoten der
WF in
gibt die Anzahl der Knoten der
WF in 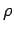 (die Null bei
(die Null bei 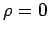 wird nicht als Knoten gezählt).
Die Zustände, die zu unterschiedlichen Werten von
wird nicht als Knoten gezählt).
Die Zustände, die zu unterschiedlichen Werten von 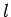 gehören, werden als s, p, d
u.s.w. für
gehören, werden als s, p, d
u.s.w. für 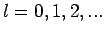 bezeichtet. Jeder Zustand mit einem bestimmten
bezeichtet. Jeder Zustand mit einem bestimmten 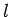 ist
ist 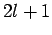 -fach nach der Werten von
-fach nach der Werten von 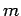 entartet. I.A. gehören zu
jedem Energieniveau mit der Hauptquantenzahl
entartet. I.A. gehören zu
jedem Energieniveau mit der Hauptquantenzahl 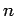 genau
genau 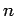 Zuständen (mit
Zuständen (mit
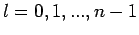 ). Diese Entartung ist nur im Coulomb-Feld vorhanden
(''zufällige Entartung).
1
Der Gesamtentartungsgrad eines stationären Zustandes ist
). Diese Entartung ist nur im Coulomb-Feld vorhanden
(''zufällige Entartung).
1
Der Gesamtentartungsgrad eines stationären Zustandes ist
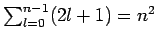 .
Die radialen Wellenfunktionen der niedrigsten Zustände sind in der folgenden
Tabelle angegeben:
.
Die radialen Wellenfunktionen der niedrigsten Zustände sind in der folgenden
Tabelle angegeben:
| Zustand |
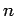 |
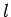 |
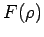 |
| 1s |
1 |
0 |
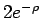 |
| 2s |
2 |
0 |
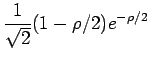 |
| 2p |
2 |
1 |
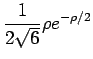 |
| 3s |
3 |
0 |
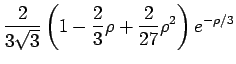 |
| 3p |
3 |
1 |
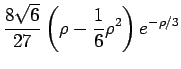 |
| 3d |
3 |
2 |
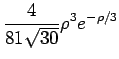 |
Subsections




Next: Mathematischer Einschub: Die zugeordneten
Up: Allgemeine Eigenschaften der Bewegung
Previous: Allgemeine Eigenschaften der Bewegung
Contents
Prof. Igor Sokolov
2005-02-14
![]() , Li
, Li![]() u.s.w. hat die radiale SGl. die Gestalt
u.s.w. hat die radiale SGl. die Gestalt
![\begin{displaymath}
-\frac{\hbar ^{2}}{2m}\frac{d^{2}}{dr^{2}}R+\left[ \frac{%
\hbar ^{2}l(l+1)}{2mr^{2}}- \frac{Ze^{2}}{r}\right]R =ER.
\end{displaymath}](img1151.png)
![]() und
und
![]() erhält man
erhält man
![]() geschrieben, wobei
geschrieben, wobei ![]() in Form einer Potenzreihe gesucht wird. Da die
Reihe nicht mit dem Glied
in Form einer Potenzreihe gesucht wird. Da die
Reihe nicht mit dem Glied ![]() anfängt, schreiben wir
anfängt, schreiben wir
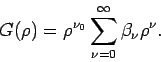
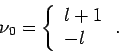
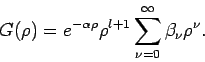
![\begin{displaymath}
\beta _{\nu +1}=\frac{2\left[ \alpha (\nu +l+1)-Z\right] }{(\nu +l+2)(\nu
+l+1)-l(l+1)}\beta _{\nu }.
\end{displaymath}](img1176.png)
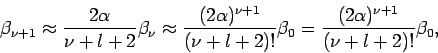
![]()
![]() ist. Daher ist
ist. Daher ist
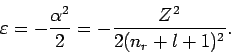

![]() ab; die Quantenzahl
ab; die Quantenzahl ![]() gibt die Anzahl der Knoten der
WF in
gibt die Anzahl der Knoten der
WF in ![]() (die Null bei
(die Null bei ![]() wird nicht als Knoten gezählt).
Die Zustände, die zu unterschiedlichen Werten von
wird nicht als Knoten gezählt).
Die Zustände, die zu unterschiedlichen Werten von ![]() gehören, werden als s, p, d
u.s.w. für
gehören, werden als s, p, d
u.s.w. für ![]() bezeichtet. Jeder Zustand mit einem bestimmten
bezeichtet. Jeder Zustand mit einem bestimmten ![]() ist
ist ![]() -fach nach der Werten von
-fach nach der Werten von ![]() entartet. I.A. gehören zu
jedem Energieniveau mit der Hauptquantenzahl
entartet. I.A. gehören zu
jedem Energieniveau mit der Hauptquantenzahl ![]() genau
genau ![]() Zuständen (mit
Zuständen (mit
![]() ). Diese Entartung ist nur im Coulomb-Feld vorhanden
(''zufällige Entartung).
1
Der Gesamtentartungsgrad eines stationären Zustandes ist
). Diese Entartung ist nur im Coulomb-Feld vorhanden
(''zufällige Entartung).
1
Der Gesamtentartungsgrad eines stationären Zustandes ist
![]() .
Die radialen Wellenfunktionen der niedrigsten Zustände sind in der folgenden
Tabelle angegeben:
.
Die radialen Wellenfunktionen der niedrigsten Zustände sind in der folgenden
Tabelle angegeben: