



Next: Heisenberg-Bild und Korrespondenzprinzip
Up: Heisenberg-Bild.
Previous: Heisenberg-Bild.
Contents
Wenn eine Messbare 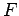 nicht explizit von der Zeit abhängt und mit dem
Hamiltonian des Systems kommutiert, so
nicht explizit von der Zeit abhängt und mit dem
Hamiltonian des Systems kommutiert, so
der entsprechende Operator ist in der Heisenbergdarstellung zeitunabhängig:
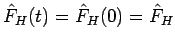 . Sein System von
Eigenvektoren ist daher auch zeitunabhängig, und die möglichen
Messergebnisse auch. Wenn die Anfangsbedingung
. Sein System von
Eigenvektoren ist daher auch zeitunabhängig, und die möglichen
Messergebnisse auch. Wenn die Anfangsbedingung
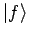 ein
Eigenwektor von
ein
Eigenwektor von 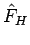 gewesen war,
gewesen war,
so blebt 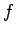 konstant. Im Schrödingerbild wäre
konstant. Im Schrödingerbild wäre 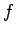 zwar konstant,
die Wellenfunktion
zwar konstant,
die Wellenfunktion
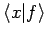 aber zeitabhängig
(Phasenmultiplikator!).
aber zeitabhängig
(Phasenmultiplikator!).
Prof. Igor Sokolov
2005-02-14
![]() nicht explizit von der Zeit abhängt und mit dem
Hamiltonian des Systems kommutiert, so
nicht explizit von der Zeit abhängt und mit dem
Hamiltonian des Systems kommutiert, so
![\begin{displaymath}
\frac{d\hat{F}_{H}}{dt}=\frac{i}{\hbar }\left[ \hat{H},\hat{F}\right] =0,
\end{displaymath}](img1804.png)