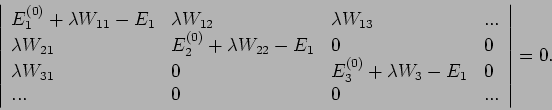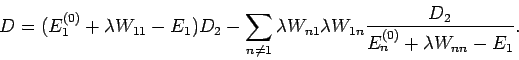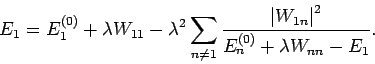Next: Entartung/Quasientartung
Up: Nichtentartetes Spektrum
Previous: Etwas andere Schreibeweise
Contents
Betrachten wir unsere Situation etwas allgemeiner. Die Schrödingergleichung
in der Energiedarstellung des ungestörten Systems
reduziert sich zu einem System homogener algebraischer Gleichungen für
die Koeffizienten 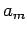 :
:
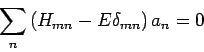 |
(54) |
mit
Das Gleichungssystem Gl.(54) hat eine Lösung falls
(die Säkulardeterminante). Die Wurzeln dieser Gleichung
ergeben das exakte Spektrum des Hamiltonians 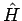 .
.
Die Determinante einer Matrix
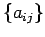 ist eine Summe über alle möglichen Produkten der Elementen aus verschiedenen Spalten
ist eine Summe über alle möglichen Produkten der Elementen aus verschiedenen Spalten
wobei
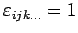 für gerade Permutationen
für gerade Permutationen 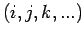 von
von 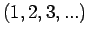 ,
,
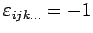 für ungerade Permutationen
und 0 falls die Indices sich wiederhohlen.
für ungerade Permutationen
und 0 falls die Indices sich wiederhohlen.
Das Suchen der Energie des Zustandes 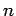 bedeutet, unsere Energie
bedeutet, unsere Energie 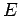 ist nahe an
ist nahe an 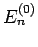 . Da alle nichtdiagonalen Elementen unserer
Determinanten
. Da alle nichtdiagonalen Elementen unserer
Determinanten 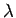 enthalten, ist die Ordnung der Störungstheorie
gleich der Anzahl der in jedem Produkt enthaltenen nichtdiagonale Terme. Die 1.
Ordnung entspricht den diagonalen Gliedern: in dieser Ordnung
enthalten, ist die Ordnung der Störungstheorie
gleich der Anzahl der in jedem Produkt enthaltenen nichtdiagonale Terme. Die 1.
Ordnung entspricht den diagonalen Gliedern: in dieser Ordnung
so dass
In der 2. Ordnung sollen wir jetzt die nichtdiagonalen Elementen mitnehmen.
Rechnen wir z.B. die Korrektur 2. Ordnung zu 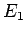 aus. Dafür ist es
genug nur die nichtdiagonalen Elementen in der 1. Zeile und 1 Spalte zu berücksichtigen:
aus. Dafür ist es
genug nur die nichtdiagonalen Elementen in der 1. Zeile und 1 Spalte zu berücksichtigen:
Die Minorenentwichlung dieses Determinanten über der 1. Spalte ergibt
(mit
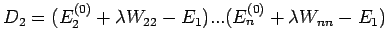 )
)
Aus der Bedingung 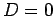 bekommen wir (unter der Voraussetzung
bekommen wir (unter der Voraussetzung 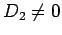 ,
keine Entartung)
,
keine Entartung)
Das ist die Gleichung für 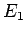 (BRILLOUIN & WIGNER) die z.B. durch der Methode der sukzessiven Approximation gelöst werden
kann. In der niedersten Ordnung (vernachlässigen
(BRILLOUIN & WIGNER) die z.B. durch der Methode der sukzessiven Approximation gelöst werden
kann. In der niedersten Ordnung (vernachlässigen
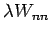 im
Nenner, Einsetzen
im
Nenner, Einsetzen
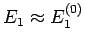 im Nenner) bekommen wir unsere
Gl.(51).
im Nenner) bekommen wir unsere
Gl.(51).




Next: Entartung/Quasientartung
Up: Nichtentartetes Spektrum
Previous: Etwas andere Schreibeweise
Contents
Prof. Igor Sokolov
2005-02-14
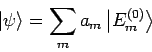
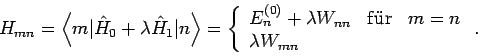
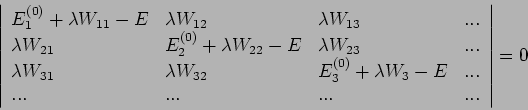
![]() ist eine Summe über alle möglichen Produkten der Elementen aus verschiedenen Spalten
ist eine Summe über alle möglichen Produkten der Elementen aus verschiedenen Spalten
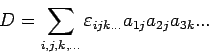
![]() bedeutet, unsere Energie
bedeutet, unsere Energie ![]() ist nahe an
ist nahe an ![]() . Da alle nichtdiagonalen Elementen unserer
Determinanten
. Da alle nichtdiagonalen Elementen unserer
Determinanten ![]() enthalten, ist die Ordnung der Störungstheorie
gleich der Anzahl der in jedem Produkt enthaltenen nichtdiagonale Terme. Die 1.
Ordnung entspricht den diagonalen Gliedern: in dieser Ordnung
enthalten, ist die Ordnung der Störungstheorie
gleich der Anzahl der in jedem Produkt enthaltenen nichtdiagonale Terme. Die 1.
Ordnung entspricht den diagonalen Gliedern: in dieser Ordnung